Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Inscrivez vous gratuitement ici....
Contenu
Tracé d’une courbe
Intersection de deux courbes
résolution graphique d’une inéquation
Ressources associées et exercices semblables
On obtient ainsi une boîte ayant la forme d'un parallélépipède rectangle de hauteur $x$ cm.
- Quelle est l'intervalle auquel doit appartenir $x$?
Aide
$x$ est une longueur donc est positif.
La boîte a une base carrée de largeur $60-2x$ et cette mesure doit être positive....Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Exprimer le volume $V(x)$ en fonction de $x$.
Aide
Rappel: le volume d'un parallélépipède rectangle de dimensions $l$, $L$ et hauteur $h$ est $V=L\times l\times h$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Avec la calculatrice, proposer une valeur de $x$ pour laquelle le volume de la boîte est maximum.
Quelle est la valeur de ce volume en dm$^3$?Aide
On peut utiliser le MENU TABLE de la calculatrice en saisissant l'expression de $V(x)$ dans Y1 et en paramétrant(SET) les les valeurs de $x$ entre 0 et 30 avec par exemple pour pas 0,5.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - On donne ci-dessous la représentation graphique de la fonction $V$.
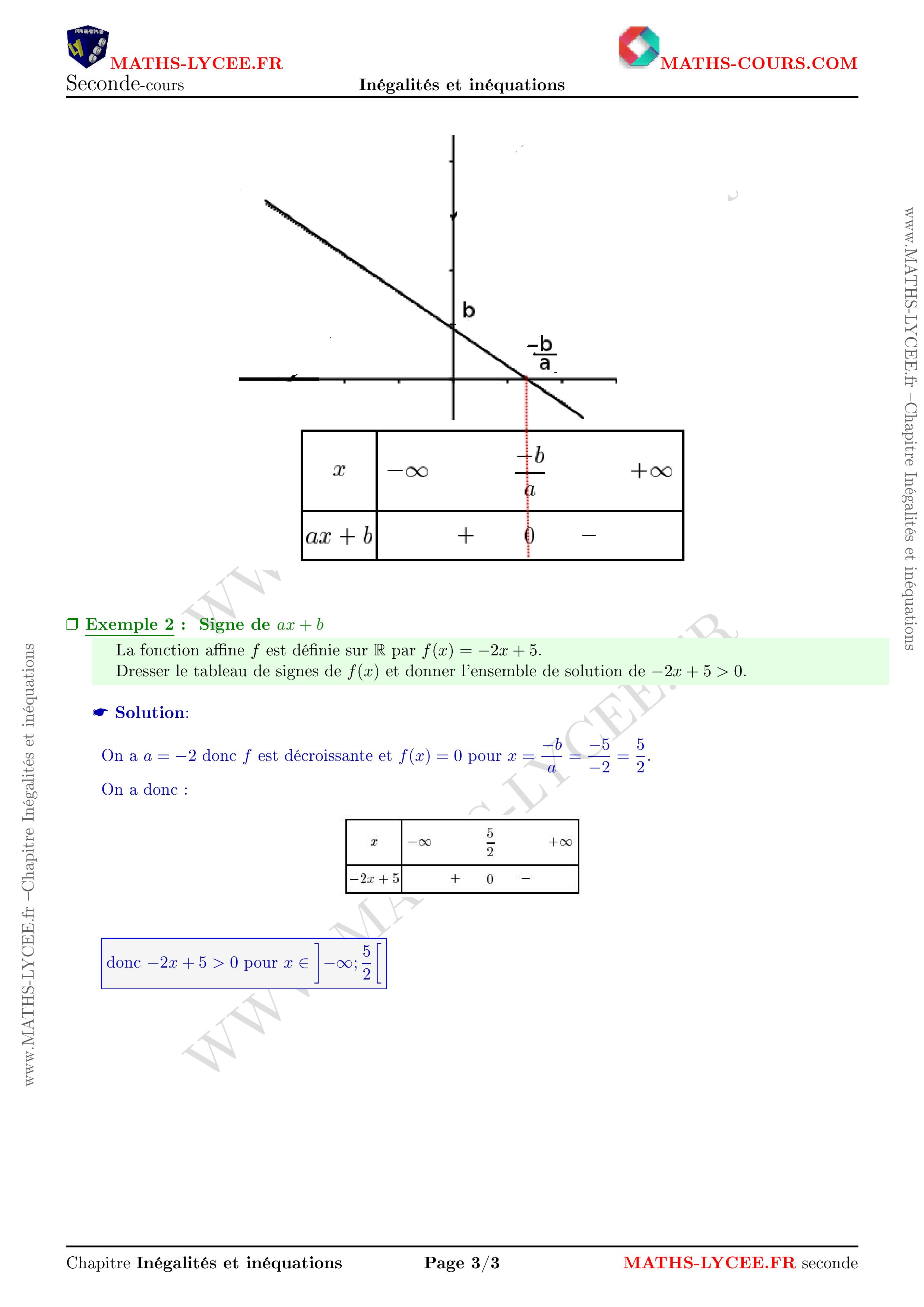
Le résultat obtenu avec la calculatrice semble-t-il cohérent avec le graphique donné?Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer graphiquement, les valeurs de $x$ pour lesquelles le volume est supérieur ou égal à 12,5 dm$^3$.
Aide
Il faut convertir 12,5 dm$^3$ en cm$^3$ et résoudre graphiquement l'inéquation correspondant à la contrainte de la question.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message