Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Inscrivez vous gratuitement ici....
Contenu
Fonction inverse: ensemble de définition, parité, variations et courbe
Ressources associées et exercices semblables
Calculs d’images et d’antécédents par la fonction inverse (réf 261)
exercice
Comparaison d’images avec la fonction inverse(réf 262)
exercice
- Rappeler l'ensemble de définition de $f$.
Solution
Il faut que le dénominateur soit différent de 0.
- Rappeler le tableau de variation de $f$.
Solution
La fonction inverse est décroissante sur $]-\infty;0[$ et décroissante sur $]0;+\infty[$.
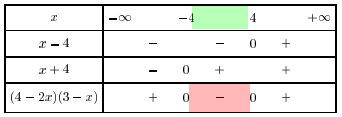
- Rappeler la parité de la fonction inverse et le justifier
Rappel cours
Fonction impaire
Une fonction $f$ définie sur $\mathbb{R}$ est impaire si pour tout réel $x$ de $D$ on a:
$\begin{cases} -x\in D\\ f(-x)=-f(x) \end{cases}$
La représentation graphique de $f$ est alors symétrique par rapport à l'origine du repère.
Remarque: pour tout réel $x\in D$ on a $-x\in D$ signifie que l'ensemble de définition est symétrique par rapport au zéro.
Par exemple si $D=[-3;5]$ la fonction $f$ ne peut pas être impaire.Solution
$D_f=\mathbb{R}^*=]-\infty;0[\cup ]0;+\infty[$
donc l'ensemble de définition est symétrique par rapport au zéro (c'est à dire que pour tout $x\in D_f$ alors on a $-x\in D_f$)
$f(-x)=(-x)^3=-x^3=-f(x)$
- Compléter le tableau de valeurs ci-dessous et tracer la courbe représentative de $f$ dans un repère orthonormal (1cm pour unité sur l'axe des abscisses et 2 cm pour unité sur l'axe des ordonnées).
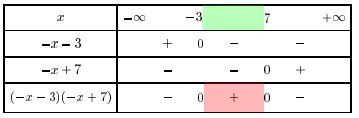
Solution

En plaçant les points de coordonnées $(x;f(x))$ dans le repère ci-dessous, on obtient la courbe représentative de $f$.
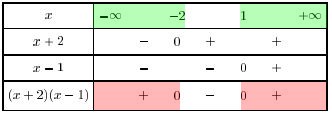


 Envoyez votre message
Envoyez votre message