Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Lecture d’un diagramme en boîte
Signification de la médiane et des quartiles
Comparaison de deux séries de données
Ressources associées et exercices semblables
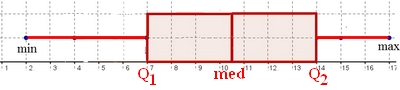
- Lire $Q_1$, $Q_3$ (premier et troisième quartile) et la médiane $m$ pour l'entreprise A puis $Q'_1$, $Q'_3$ et la médiane $m'$ pour l'entreprise B.
Rappel cours
Diagramme en boîte
Sur un axe gradué, on doit placer le minimum, $Q_1$, médiane, $Q_3$ et la valeur maximale.
Solution
- Donner une interprétation de la valeur de $Q_1$, $Q_3$.
Rappel cours
Quartiles
Le premier quartile $Q_1$ est la plus petite valeur du caractère telle que au moins 25% (un quart) des valeurs soient inférieures ou égales à $Q_1$.
Le troisième quartile $Q_3$ est la plus petite valeur du caractère telle que au moins 75% (trois quarts) des valeurs soient inférieures ou égales à $Q_3$.
L'intervalle $[Q_1;Q_3]$ est l'intervalle interquartile et $Q_3-Q_1$ est l'écart interquartile.Solution
$Q_1=4$ donc au moins 25% des salariés de l'entreprise A ont un salaire annuel inférieur ou égal à 40 000 euros.
$Q_3=12$ donc au moins 75% des salariés de l'entreprise A ont un salaire annuel inférieur ou égal à 120 000 euros. - Que peut-on conclure pour les salaires de ces deux entreprises à la lecture de ces deux diagrammes?
Solution
La médiane est identique pour les deux entreprises donc dans les deux cas, la moitié des salariés gagnent moins de 100 000 euros.
Mais $Q_1$<$Q'1$ et $Q_3$<$Q'3$ donc les salaires sont plus élevés dans l'entreprise B que dans A puisque
au moins 25% des salariés de A gagnent moins de 40 000 euros alors que c'est moins de 60 000 euros pour B.
De même, au moins 75% des salariés de A gagnent moins de 120 000 euros alors que c'est moins de 140 000 euros pour B.