Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Signe d’un polynôme de degré 2
Tableau de signes d’un produit ou d’un quotient
Ressources associées et exercices semblables
Inéquations avec un quotient (réf 483)
exercice
Inéquation de degré 3 (réf 0487)
exercice
Vidéo de l’exercice
- Résoudre $(2x^2-6x-1)(x^2+9x-10)>0$
Rappel cours
Signe de $ax^2+bx+c$
- Cas $\Delta>0$ (deux racines $x_1$ et $x_2$

- Cas $\Delta=0$ (une racine $x_1$)
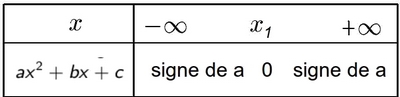
- Cas $\Delta<0$ (aucune racine)
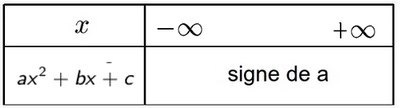 Somme et produit des racines
Somme et produit des racines
Si le polynôme $P(x)=ax^2+bx+c$ (avec $a\neq 0$) admet deux racines $x_1$ et $x_2$ alors on a:
$ x_1+x_2=\dfrac{-b}{a}$ (somme des racines)
et $x_1x_2=\dfrac{c}{a}$ (produit des racines)Aide
Il faut utiliser un tableau de signes avec le produit des facteurs $2x^2-6x-1$ et $x^2+9x-10$
Rechercher les racines de chaque facteurSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Résoudre $\dfrac{x^2+3x-4}{-x^2+5x-6}\leq 0$
Aide
Il faut utiliser un tableau de signes avec le quotient de $x^2+3x-4$ et $-x^2+5x-6$
il y a deux valeurs interdites (double barre)Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message