Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Dérivée et variation d’un polynôme de degré 3
Recherche du bénéfice maximum
Étude du coût moyen
Ressources associées et exercices semblables
Recettes, coûts et recherche d’un bénéfice maximal (réf 0565)
exercice
Le prix de vente d'un litre de ce produit chimique est de 2300 euros.
- Montrer que la recette est donnée par la fonction $R$ définie sur $I$ par $R(x)=23x$
Aide
es quantités sont données en litres
Exprimer cette recette en centaines d'euros.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer la quantité à produire pour que le bénéfice soit maximal.
Aide
Etudier le signe de la dérivée de la fonction $B$ puis les variations pour déterminer l'extremum de $B$
Solution
Vous devez être abonné pour accéder à ce contenu...
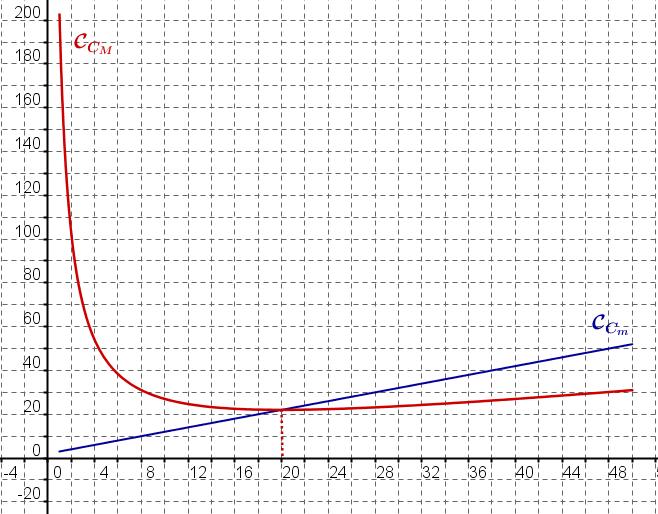
Infos abonnements - Le coût moyen de production d'un litre quand on en produit $x$ litres est la fonction notée $C_M$ et définie par $C_M(x)=\dfrac{C(x)}{x}$ avec $x\in [1;50]$
Exprimer le coût moyen de production en fonction de $x$ et en déduire la quantité à produire, arrondie à 0,1 litre près, pour obtenir un coût moyen minimum.Aide
Calculer $C_M'(x)$ puis étudier les variation de la fonction $C_M$ pour déterminer le minimum de la fonction $C_M$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Le coût marginal de production est le supplément de coût total de production engendré par la production d'un litre supplémentaire.
Si on note $C_m(x)$ ce coût marginal, on a alors $C_m(x)=C(x+1)-C(x)$
Calculer alors le coût marginal pour une production de 20 litres, c'est à dire l'augmentation du coût total de production pour passer de 20 litres à 21 litres.
Calculer $C'(20)$ et comparer les deux résultats.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En pratique, on assimile le coût marginal de production pour une quantité $x$ à la dérivée du coût total.
On a en effet $C_m(x)=\dfrac{C(x+1)-C(x)}{x+1-x}$ (taux d'accroissement de $C$ entre $x+1$ et $x$).
Résoudre l'équation $C_M(x)=C_m(x)$.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Complément: Graphiquement le coût moyen de production est minimum pour une production correspondant à l'abscisse du point d'intersection des courbes représentatives des fonctions coût marginal et coût moyen.


 Envoyez votre message
Envoyez votre message