Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Détermination graphique des termes d’une suite définie sous forme explicite
Ressources associées et exercices semblables
Calculs des termes d’une suite sous forme explicite (réf 0582)
exercice
Calcul des termes d’une suite définie par récurrence (réf 0585)
exercice
Détermination graphique des termes d’une suite (réf 0588)
exercice
Vidéo de l’exercice
- $u_{n}=3n+2$
Rappel cours
Fonction affine
Une fonction afffine est définie sur $\mathbb{R}$ par $f(x)=ax+b$.
La représentation graphique d'une fonction affine est une droite coupant l'axe des ordonnées au point $(0;b)$ et l'axe des abscisses au point $\left(\dfrac{-b}{a}\right)$ (si $a\neq 0$).
Si $a=0$ alors la droite est parallèle à l'axe des abscisses.Aide
Si $f$ est la fonction associée à la suite $(u_{n })$, on a $u_{n}=f(n)$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - $u_{n}=n^2-4n+2$
Rappel cours
Forme canonique
Toute fonction polynôme de degré 2 définie sur $\mathbb{R}$ par $P (x) = ax^2 + bx + c$ peut s'écrire sous la forme $P (x) = a(x -\alpha)^2 + \beta$ avec $\alpha=\dfrac{-b}{2a}$ et $\beta= P ( \alpha)$.
Cette écriture de $P (x)$ est appelée forme canonique et $S(\alpha;\beta)$ est le sommet de la parabole représentant la fonction $P$
Parabole
La représentation graphique d'une fonction polynôme de degré 2 est une parabole.
$S$ est le sommet de la parabole.
Si $P(x)=ax^2+bx+c$ on a:
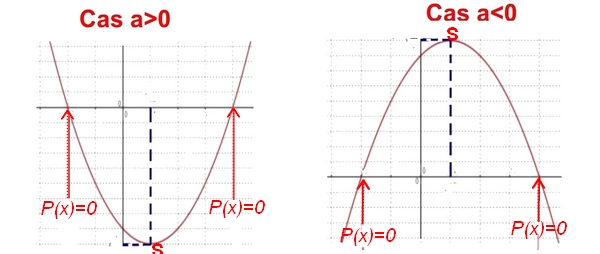
Aide
La représentation graphique de $f$ est une parabole
On peut déterminer les coordonnées du sommet puis utiliser la calculatrice pour dresser un tableau de valeurs de la fonction et placer suffisamment de points pour obtenir un tracé précisSolution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION


 Envoyez votre message
Envoyez votre message