Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Angles de références sur le cercle trigonométrique
Angles associés
Ressources associées et exercices semblables
Calcul d’un angle correspondant à un point du le cercle trigonométrique (réf 0706)
exercice
Points confondus sur le cercle trigonométrique (réf 0708)
exercice
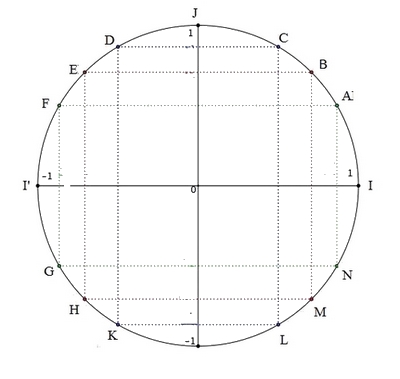
Les réels associés respectivement aux points $A$, $B$ et $C$ sont $\dfrac{\pi}{6}$, $\dfrac{\pi}{4}$ et $\dfrac{\pi}{3}$.
- En utilisant les symétriques de $A$, $B$ et $C$ par rapport à l'axe des abscisses, déterminer les réels de $]-\pi;\pi ]$ associés aux points $L$, $M$ et $N$.
Aide
L'enroulement se fait dans le sens indirect
Pour le point $N$, on a $\widehat{IOA}=\widehat{ION}$Solution
$N$ est le symétrique de $A$ par rapport à l'axe des abscisses $(OI)$
donc $\widehat{IOA}=\widehat{ION}$.
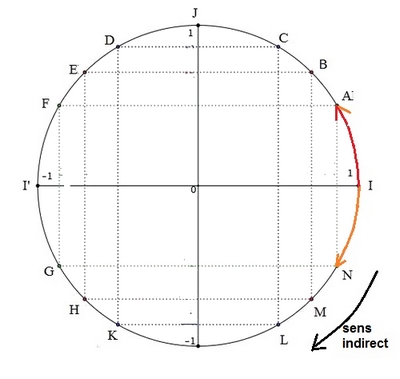
Pour le point $N$, l'enroulement se fait dans le sens indirect
De même, le réel de $]-\pi;\pi]$ associé à $M$ est $\dfrac{-\pi}{4}$ et celui associé à $L$ est $\dfrac{-\pi}{3}$ - En utilisant les symétriques de $A$, $B$ et $C$ par rapport à l'axe des ordonnées, déterminer les réels de $]-\pi;\pi ]$ associés aux points $D$, $E$ et $F$.
Aide
Pour le point $D$, on a $\widehat{IOC}=\widehat{I'OD}$
Solution
$D$ est le symétrique de $C$ par rapport à l'axe des ordonnées $(OJ)$
donc $\widehat{IOC}=\widehat{I'OD}$.
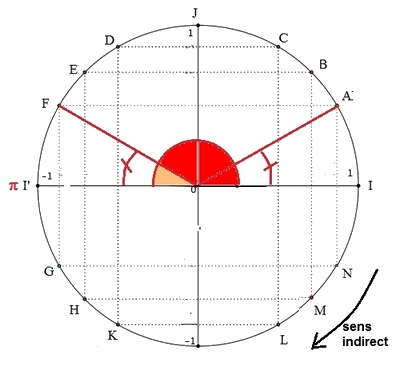
$\widehat{IOD}=\widehat{IOI'}-\widehat{I'OD}$
soit $\pi-\dfrac{\pi}{6}=\dfrac{6\pi}{6}-\dfrac{\pi}{6}=\dfrac{5\pi}{6}$
De même, le réel de $]-\pi;\pi]$ associé à $M$ est $\pi-\dfrac{\pi}{4}=\dfrac{3\pi}{4}$
et celui associé à $L$ est $\pi-\dfrac{\pi}{3}=\dfrac{2\pi}{3}$ - En utilisant les symétriques de $D$, $E$ et $F$ par rapport à l'axe des abscisses, déterminer les réels de $]-\pi;\pi ]$ associés aux points $G$, $H$ et $K$.
Aide
L'enroulement se fait dans le sens indirect
Solution
$G$ est le symétrique de $F$ par rapport à l'axe des abscisses $(OI)$
donc $\widehat{IOF}=\widehat{IOG}$.
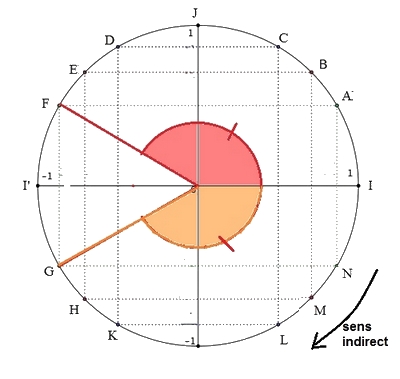
Pour le point $G$, l'enroulement se fait dans le sens indirect
De même, le réel de $]-\pi;\pi]$ associé à $H$ est $\dfrac{-3\pi}{4}$ et celui associé à $K$ est $\dfrac{-2\pi}{3}$