Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Ensemble de définition d’une fonction
Composition avec exponentielles
Recherche des limites aux bornes de l’ensemble de définition et interprétation graphique
Ressources associées et exercices semblables
Limites par composition (réf 1003)
exercice
Limites par composition avec exponentielle (réf 1004)
exercice
- Déterminer l'ensemble de définition de $f$
Aide
On ne peut pas diviser par $0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer la limite en $+\infty$.
Rappel cours
composition de deux fonctions
Soient $u$ et $v$ deux fonctions définies sur $I$ et $J$ avec $u(x)\in J$ pour tout $x\in I$, la composée de $u$ par $v$ notée $vou$ est la fonction définie sur $I$ par $vou(x)=v(u(x))$.
Par exemple avec $v(x)=x^2$ et $u(x)=5x$ on a $f(x)=vou(x)=v(u(x))=v(5x)=(5x)^2$Aide
On pose $u(x)=\dfrac{-1}{x+2}$ et $v(x)=e^x$ pour utiliser la limite par composition
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer limite en $ -2^+$
Aide
on utilise de nouveau la composition de deux fonctions
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer limite en $ -2^+$
Aide
on utilise de nouveau la composition de deux fonctions
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer la limite en $-\infty$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Donner les asymptotes à la courbe représentative de $f$
Rappel cours
limite $l$ en $+\infty$ et interprétation graphique
La fonction $f$ est définie sur un intervalle $[a;+\infty[$ et $\ell \in \mathbb{R}$.
$\displaystyle \lim_{x \rightarrow +\infty}f(x)=\ell$ si pour tout intervalle ouvert I contenant $\ell$, il existe $x_0$ tel que pour tout $x>x_0$ on a $f(x)\in $ I
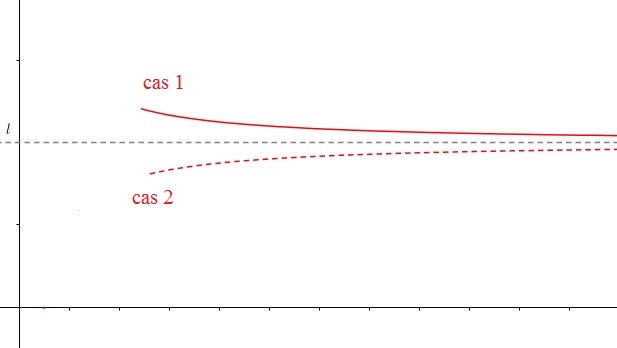
La droite d'équation $y=\ell$ est asymptote à la courbe en $+\infty$
Limite infinie quand $x \longrightarrow a$
$f$ est définie sur un intervalle $I$ contenant $a$.
$\displaystyle \lim_{x \rightarrow a}f(x)=+\infty$ si pour tout réel $A>0$, il existe un réel $\epsilon>0$ avec $]a-\epsilon;a+\epsilon[\subset I$ tel que $f(x)>A$ pour tout $x\in ]a-\epsilon;a+\epsilon[$.
La droite d'équation $x=a$ est asymptote à a courbe.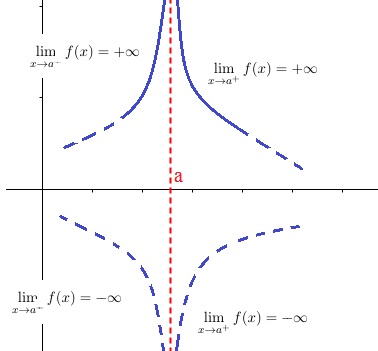
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Contrôler ces résultats en traçant la courbe sur la calculatrice
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message