Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Limites et interprétation graphique
Asymptotes
Centre de symétrie d’une hyperbole
Ressources associées et exercices semblables
Interrogation opérations sur les limites (réf 1015)
devoir
Limites, cas d’indétermination et asymptotes (réf 1016)
devoir
- Déterminer les limites de $f$ aux bornes de $D_f$.
Rappel cours
limites usuelles
$\displaystyle \lim_{x \rightarrow +\infty}x^n=+\infty$ ($n\in \mathbb{N}^*$)
$\displaystyle \lim_{x \rightarrow +\infty}\dfrac{1}{x^n}=0$ ($n\in \mathbb{N}^*$)
$\displaystyle \lim_{x \rightarrow 0}\dfrac{1}{x^n}=\pm \infty$ ($n\in \mathbb{N}^*$)
Limites de la fonction exponentielle(vue en première)
$\displaystyle \lim_{x \rightarrow -\infty}e^x=0$
$\displaystyle \lim_{x \rightarrow +\infty}e^x=+\infty$ $\displaystyle \lim_{x \rightarrow -\infty}x^n=\pm \infty$ ($n\in \mathbb{N}^*$)
$\displaystyle \lim_{x \rightarrow -\infty}\dfrac{1}{x^n}=0$ ($n\in \mathbb{N}^*$)
$\displaystyle \lim_{x \rightarrow +\infty}\sqrt{x}=+ \infty$ ($n\in \mathbb{N}^*$)
Limites de la fonction $ln$ (chapitre fonction $ln$)
$\displaystyle \lim_{x \rightarrow 0^+}ln(x)=-\infty$
$\displaystyle \lim_{x \rightarrow +\infty}ln(x)=+\infty$
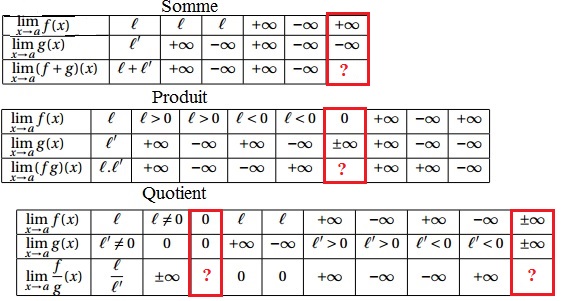
Opérations sur les limites
Aide
Pour les limites en $+\infty$ et $-\infty$, il faut factoriser $x$ au numérateur et au dénominateur
Pour la limite en $x=1$, il faut distinguer les cas $x< 1$ et $x > 1$Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - En déduire les asymptotes à la courbe $C_f$.
Rappel cours
limite $l$ en $+\infty$ et interprétation graphique
La fonction $f$ est définie sur un intervalle $[a;+\infty[$ et $\ell \in \mathbb{R}$.
$\displaystyle \lim_{x \rightarrow +\infty}f(x)=\ell$ si pour tout intervalle ouvert I contenant $\ell$, il existe $x_0$ tel que pour tout $x>x_0$ on a $f(x)\in $ I
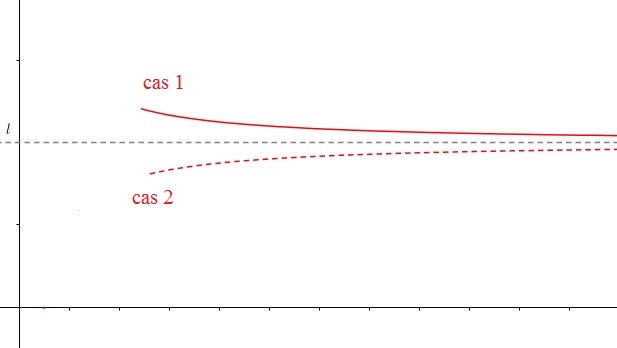
La droite d'équation $y=\ell$ est asymptote à la courbe en $+\infty$
Limite infinie quand $x \longrightarrow a$
$f$ est définie sur un intervalle $I$ contenant $a$.
$\displaystyle \lim_{x \rightarrow a}f(x)=+\infty$ si pour tout réel $A>0$, il existe un réel $\epsilon>0$ avec $]a-\epsilon;a+\epsilon[\subset I$ tel que $f(x)>A$ pour tout $x\in ]a-\epsilon;a+\epsilon[$.
La droite d'équation $x=a$ est asymptote à a courbe.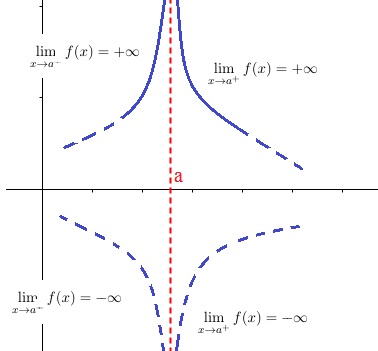
Aide
Utiliser les limites obtenues à la question précédente
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - On note $C$ le point d'intersection des deux asymptotes.
Déterminer les coordonnées de $C$.
Soit $M(x;y)$ un point du plan, $M'$ est le symétrique de $M$ par rapport à $C$.
Exprimer les coordonnées de $M'$ en fonction de $x$ et $y$.Aide
$C$ est le milieu de $[MM']$.
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Montrer que si $M\in C_f$ ($x\neq 1$) alors $M' \in C_f$.
Aide
Si $M\in C_f$ on a $y=f(x)$.
On veut montrer que $y_{M'}=f(x_{M'})$Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Que peut-on en déduire pour la courbe $C_f$?
On donne ci-dessous le tracé de $C_f$ sur $]1;+\infty[$.
Terminer le tracé de $C_f$ et tracer les deux asymptotes à la courbe.
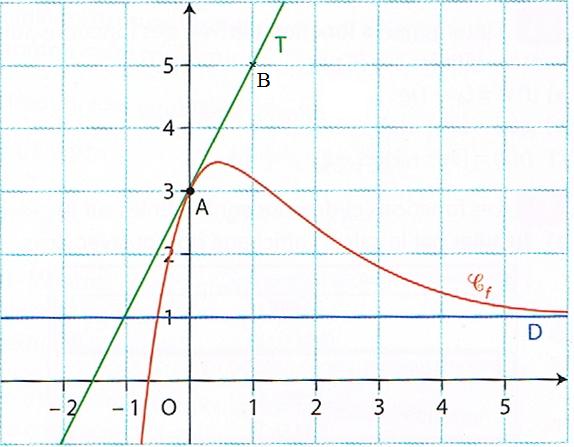
Aide
Si $M\in C_f$, son symétrique par rapport à $C$ appartient à $C_f$.
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION


 Envoyez votre message
Envoyez votre message