Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Matrice d’un graphe
Matrice puissance 3 à la calculatrice
Nombre de chaînes de longueur 3 sur un graphe
Ressources associées et exercices semblables
Matrice d’un graphe et d’un graphe orienté (réf 1651)
exercice
Matrice d’un graphe, chaînes de longueur n sur un graphe (réf 1652)
exercice
Matrice d’un graphe et nombre de chaînes de longueur 3 (réf 1654)
exercice
- Donner la matrice de ce graphe (en ordonnant les sommets dans l'ordre alphabétique).

Rappel cours
Matrice associée à un graphe
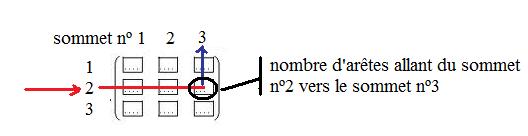
La matrice associée à un graphe d'ordre $n$ dont les sommets sont numérotés de 1 à n est une matrice carrée de dimension $n$, où le terme à l'intersection de la iième ligne et de la jième colonne est nombre d'arêtes reliant i et j.
Cette matrice est appelée matrice d'adjacence du graphe.
Aide
Il y a 5 sommets donc la matrice est une matrice carrée d'ordre 5
Les coefficients de la première ligne correspondent aux arêtes partant du sommet ASolution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Avec la calculatrice, calculer $M^3$.
En déduire le nombre de chaînes de longueur 3 allant du sommet B au sommet E.Rappel cours
Nombre de chemins de longueur $p$
Nombre de chaînes de longueur $p$}{Soit $G$ un graphe d'ordre $n$ et de matrice d'adjacence $M$.
Le coefficient $m_{ij}$ de la matrice $M^p$ ($p$ entier naturel non nul) est le nombre de chaînes de longueur $p$ reliant les sommets $i$ et $j$.}Aide
avec la calculatrice, saisir les coefficients de $M$ puis calculer $M^3$ (OPTN puis MAT puis MAT A$^3$)
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION


 Envoyez votre message
Envoyez votre message