Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Calculs de probabilités avec un arbre
Établir la loi de probabilités d’une variable aléatoire
Calcul de l’espérance
Ressources associées et exercices semblables
Calcul de probabilités, loi de probabilité et espérance (réf 0890)
exercice
Aie mémoire probabilités et variables aléatoires (réf 0903)
mémo
Cette bille roule sur un plan comportant une cible circulaire évidée en son centre. Lorsque la bille atteint la cible, soit elle est avalée, soit elle reste sur la cible.
Lorsque la bille n'atteint pas la cible elle revient à son point de départ et le jeu s'arrête.
Dans la suite de l'exercice, on notera :
- C l'événement "la cible est atteinte";
-B l'événement "la bille est avalée".
Une étude préliminaire a démontré que :
-la probabilité d'atteindre la cible lors d'un lancer est égale à $0,3$ ;
-lorsque la cible a été atteinte, la probabilité que la bille soit avalée est égale à 0,2.
- Traduire la situation aléatoire ci-dessus par un arbre de probabilité.
Rappel cours
Arbre pondéré
Probabilités sur un arbre pondéré:
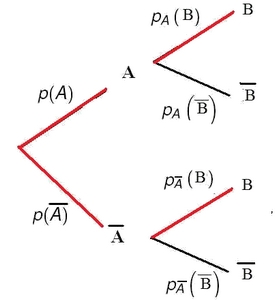
Aide
Traduire d'abord les données de l'énoncé avec les notations des événements et des probabilités
Les probabilités non conditionnelles sont à placer au premier niveau de l'arbreSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Calculer la probabilité $P_{1}$ que la bille soit avalée.
Rappel cours
Probabilité conditionnelle
Soient $A$ et $B$ deux événements avec $p(A)\neq 0$.
La probabilité que l'événement $B$ soit réalisé sachant que l'événement $B$ est réalisé se note $p_A(B)$
et on a $p_A(B)=\dfrac{p(A\cap B)}{p(A)}$.Aide
La probabilité $P_{1}$ que la bille soit avalée se note $p(C\cap B)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Calculer la probabilité $P_{2}$ qu'elle reste sur la cible.
Aide
La probabilité $P_{2}$ que la bille soit avalée se note $p(C\cap \overline{B})$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Une partie se déroule selon la règle ci-dessous.
Pour jouer, on paie $0,50$~euro et on actionne le bouton qui lance la bille :
-si la bille est avalée, on gagne un lot d'une valeur de $g$ euros ;
-si la bille reste sur la cible sans être avalée, on est remboursé ;
-si la bille rate la cible, on perd la mise.
Déterminer complètement la loi de probabilité de gain d'un joueur (on recopiera et on complétera le tableau ci-dessous).

Aide
Déterminer les valeurs prises par la variable en utilisant tous les parcours possibles sur l'arbre.
On mise 0,5 euro au départ donc cette somm est à soustraire du gainfatSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Montrer que l'espérance de gain d'un joueur en fonction de $g$ est $E= 0,06g - 0,38$.
Rappel cours
Espérance-variance-écart type
L'espérance de la variable aléatoire $X$ (avec les notations précédentes) est:
$E(X)=x_1p_1+x_2p_2+......+x_np_n=\sum_{i=1}^n p_ix_i$
La variance d'une variable aléatoire $X$ est:
$V(X)=p_1(x_1-E(X))^2+p_2(x_2-E(X))^2+.....+p_n(x_n-E(X))^2=\sum_{i=1}^n p_i(x_i-E(X))^2$
ou bien $V(X)=p_1x_1^2+p_2x_2^2+.....+p_nx_n^2-(E(X))^2=\sum_{i=1}^n p_ix_i^2-(E(X))^2$
L'écart type est égal à la racine carrée de la variance: $\sigma(X)=\sqrt{V(X)}$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - On prévoit qu'un grand nombre de parties seront jouées.
Pour quelles valeurs de $g$ les organisateurs peuvent-ils espérer un bénéfice ?
Donner la valeur maximale de $g$ arrondie aux centimes d'euros.Aide
Pour que les organisateurs ne perdent pas d'argent, il faut que $E(X)\leqslant 0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message