Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Dérivée de exp(kx)
Tableau de variation
Recherche d’antécédents
Ressources associées et exercices semblables
Étude d’une fonction avec exp(kx), courbe et tangente (réf 0674)
exercice
Partie A
Cet investissement se déprécie (perd de sa valeur). Sa dépréciation cumulée, en milliers d'euros, a l'instant $x$, mesuré en années, est notée $D(x)$. On pose $D(x)= 200\left(1 - e^{-0,086x}\right)$ pour tout réel $ x$ de l'intervalle I = [0 ; 13].
On donne ci-dessous la courbe représentative de $D$ dans le plan rapporté à un repère orthogonal.

Déterminer graphiquement au cours de quelle année l'investissement aura perdu 60% de sa valeur (faire apparaître sur le graphique les tracés qui permettent d'obtenir la réponse).
Aide
60% de 200=$\dfrac{60\times 200}{100}=120$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Partie B
Le transporteur veut revendre l'autocar. On note $V(x)$ la valeur de l'autocar l'année $x$, $ 0 \leqslant x \leqslant 13$.
- Vérifier que $V(x) = 200 \times e^{-0,086x}$.
Aide
La valeur de revente est la valeur initiale moins la perte de valeur
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Étudier le sens de variation de $V$ sur $[0 ; 13]$.
Rappel cours
Dérivée de $exp(x)$ et de $exp(kx)$
La fonction $exp$ est dérivable sur $\mathbb{R}$ et $(exp(x))'=exp(x)$
La fonction $f$ définie par $f(x)=exp(kx)=e^{kx}$ avec $k$ réel est dérivable sur $\mathbb{R}$ et $f'(x)=kexp(kx)=ke^{kx}$Aide
Il faut calculer $V'(x)$
$e^{-0,086x}>0$ pour tout réel $x$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Combien peut-on espérer revendre l'autocar au bout de $13$ ans de service ? (au millier d'euros près).
Aide
Il faut calculer $V(13)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Graphiquement, déterminer cours de quelle année l'autocar a-t-il perdu la moitié de sa valeur et contrôler avec la calculatrice ?
Aide
On veut que la valeur de revente soit inférieure ou égale à 100
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements Il faut résoudre graphiquement $V(x)=100$
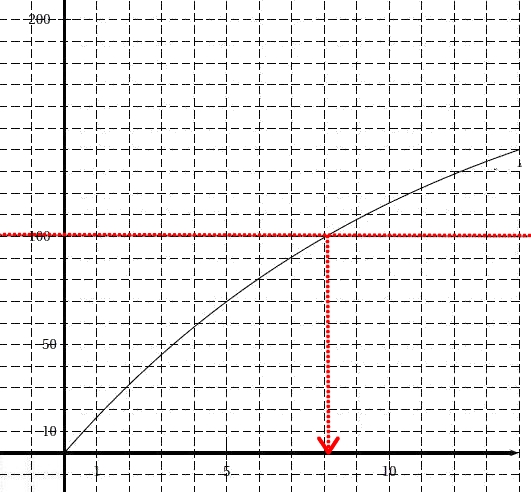
donc l'équation $V(x)=100$ admet une solution unique $\alpha$ comprise dans l'intervalle $[8;9]$.
$V(8)= 200\times e^{-0,086\times 8}\approx 100,5$
$V(9)= 200\times e^{-0,086\times 9}\approx 92,2$
donc $V(8)>100$ et $V(9)<100$ [/pms-restrict]


 Envoyez votre message
Envoyez votre message