Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Déterminer la forme canonique et en déduire le tableau de variation
Vérifier des racines
Déterminer la forme factorisée
Ressources associées et exercices semblables
Déterminer la forme canonique et la forme factorisée (réf 0490)
exercice
Déterminer la forme factorisée à partir de la parabole (réf 0476)
exercice
Méthode recherche de l’expression de f connaissant la parabole (réf 0517)
méthode
Vidéo de l’exercice
- Déterminer la forme canonique de $f$.
Rappel cours
Forme canonique
Toute fonction polynôme de degré 2 définie sur $\mathbb{R}$ par $P (x) = ax^2 + bx + c$ peut s'écrire sous la forme $P (x) = a(x -\alpha)^2 + \beta$ avec $\alpha=\dfrac{-b}{2a}$ et $\beta= P ( \alpha)$.
Cette écriture de $P (x)$ est appelée forme canonique et $S(\alpha;\beta)$ est le sommet de la parabole représentant la fonction $P$Aide
Il faut alors calculer $\alpha$ et $\beta=f(\alpha)$ avec $a=2$, $b=-4$ et $c=-6$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Dresser le tableau de variations de $f$
Rappel cours
Variations fonction polynôme du second degré
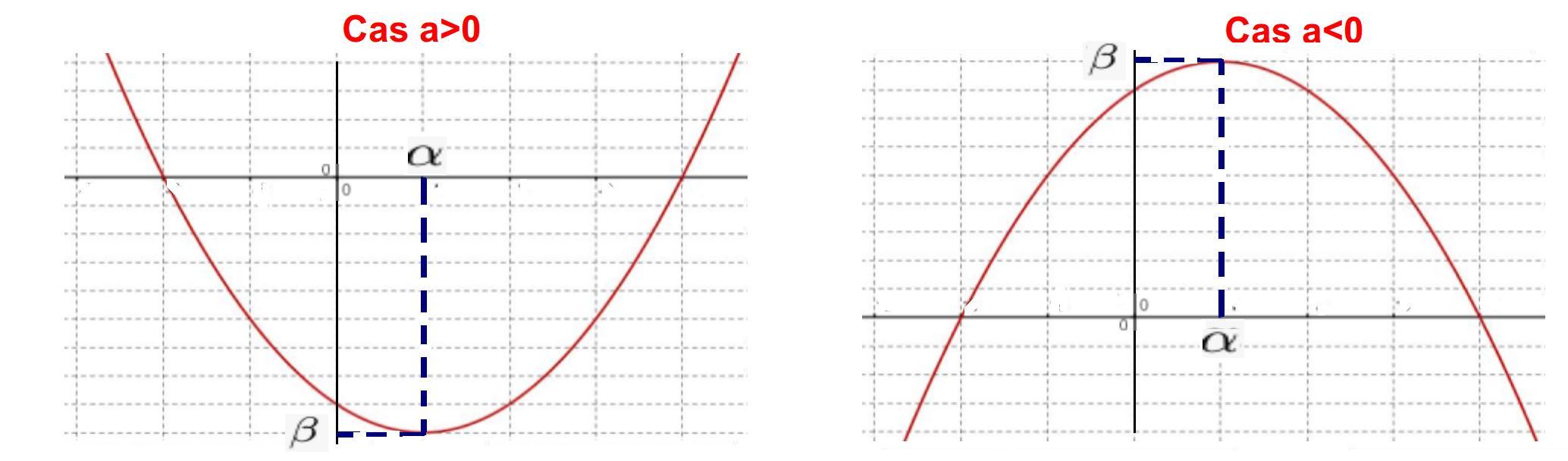
Soit la fonction $P$ définie sur $\mathbb{R}$ par sa forme canonique $P (x) = a(x-\alpha)^2 + \beta$
La courbe représentative de $P$ est une parabole dont le sommet a pour coordonnées $(\alpha; \beta)$.
Tableau de variation: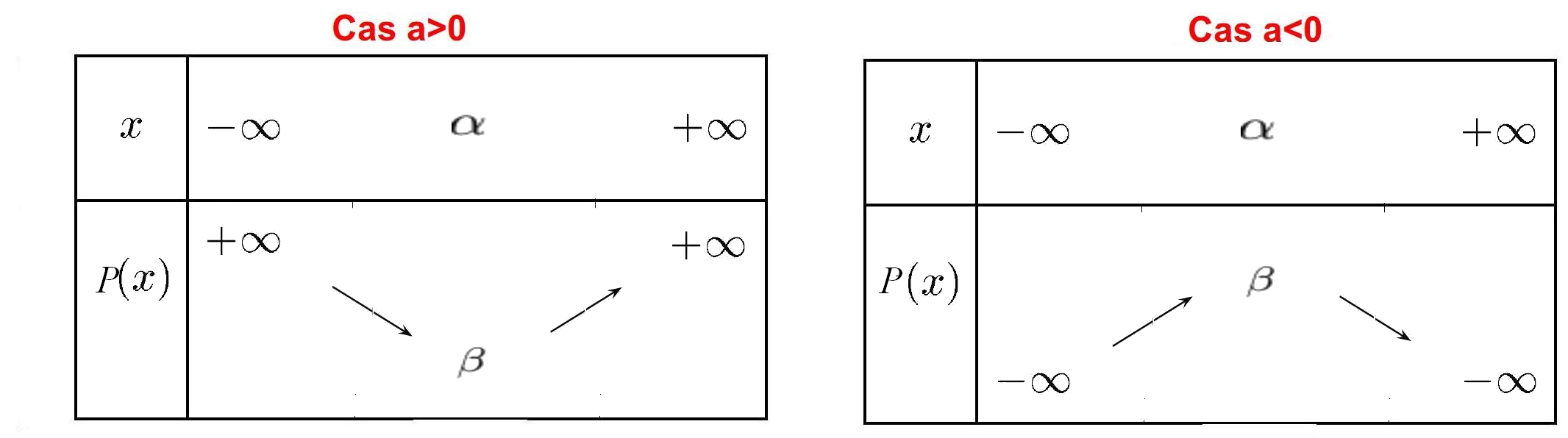
Aide
Il faut alors calculer $\alpha$ et $\beta=f(\alpha)$ avec $a=2$, $b=-4$ et $c=-6$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Montrer que $x_1=-1$ et $x_2=3$ sont deux racines de $f$.
Rappel cours
Racines
Les racines de $p(x)=ax^2+bx+c$ avec$a\neq 0$ sont les valeurs de $x$ annulant $P$
c'est à dire telles que $P(x)=0$.
$\Delta=b^2-4ac$
Si $\Delta>0$ donc il y a deux racine $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}$
Si $\Delta=0$ il y a une racine (double) $x_1=\dfrac{-b}{2a}$
Si $\Delta<0$ il n'y a aucune racine
Remarque: Graphiquement, les racines sont les abscisses des points d'intersection de la parabole et de l'axe des abscisses.Aide
Il faut vérifier que $f(x_1)=0$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Vérifier que la forme factorisée de $f$ est $f(x)=a(x-x_1)(x-x_2)$.
Rappel cours
Identités remarquables
$(a+b)^2=a^2+2ab+b^2$
$(a-b)^2=a^2-2ab+b^2$
$(a-b)(a+b)=a^2-b^2$
Aide
Remplacer $x_1$ et $x_2$ par les valeurs obtenues à la question précédente et vérifier que l'on obtient $2x^2-4x-6$ en développant.
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION


 Envoyez votre message
Envoyez votre message