Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Forme canonique et variations
Équations de degré 2
Tableau de signes d’un polynôme de degré 2
Résolution d’inéquations
Problème de recettes-coûts et bénéfices
Ressources associées et exercices semblables
Méthode équations du second degré commentées (réf 0518)
méthode
Vous répondrez sur la copie en notant la lettre correspondant à votre réponse.
Chaque question est notée sur 1 point.
Une réponse fausse enlève 0,5 point et l'absence de réponse donne 0 point.
Si le total des points est négatif, l'exercice est noté sur 0 point.
- La fonction $f$ est définie sur $\mathbb{R}$ par $ f(x)=2(x+3)^2+12$.
La parabole représentant $f$ a pour sommet
a. $S(3;12)$
b. $ S(-3;-12)$
c. $S(-3;12)$Rappel cours
Forme canonique
Toute fonction polynôme de degré 2 définie sur $\mathbb{R}$ par $P (x) = ax^2 + bx + c$ peut s'écrire sous la forme $P (x) = a(x -\alpha)^2 + \beta$ avec $\alpha=\dfrac{-b}{2a}$ et $\beta= P ( \alpha)$.
Cette écriture de $P (x)$ est appelée forme canonique et $S(\alpha;\beta)$ est le sommet de la parabole représentant la fonction $P$Aide
Identifier $\alpha$ et $\beta$ dans la forme canonique donnée ci-dessus.
On veut avoir dans les parenthèses $x-\alpha$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - La fonction $f$ définie sur $\mathbb{R}$ par $ f(x)=x^2-x+3$ est de signe
a. positif
b. négatif
c. on ne peut pas le savoirRappel cours
Signe de $ax^2+bx+c$
- Cas $\Delta>0$ (deux racines $x_1$ et $x_2$

- Cas $\Delta=0$ (une racine $x_1$)
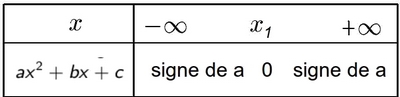
- Cas $\Delta<0$ (aucune racine)
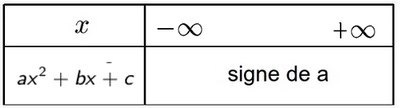
Aide
Déterminer s'il y en a les racines du polynôme pour connaître son signe.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - La fonction $f$ définie sur $\mathbb{R}$ par $ f(x)=2x^2-16x+14$ a pour forme factorisée
a. $f(x)=2(x-1)(x-7)$
b. $ f(x)=(x-1)(x-7)$
c. $ f(x)=2(x+1)(x+7)$Rappel cours
Forme factorisée
- Si le polynôme du second degré $P(x)=ax^2+bx+c$ (avec $a\neq 0$) admet deux racines $x_1$ et $x_2$
alors la forme factorisée de $P$ est $P(x)=a(x-x_1)(x-x_2)$
- Si le polynôme du second degré $P(x)=ax^2+bx+c$ (avec $a\neq 0$) admet une racine $x_1$
alors la forme factorisée de $P$ est $P(x)=a(x-x_1)^2$
- Si le polynôme du second degré $P(x)=ax^2+bx+c$ (avec $a\neq 0$) n'admet aucune racine
alors la forme factorisée de $P$ n'existe pasAide
On peut déterminer les racines de $f(x)$ pour écrire la forme factorisée
On peut aussi développer chacune des expressions proposéesSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Déterminer les racines du polynôme $x^2-6x+5$.
Rappel cours
Racines
Les racines de $p(x)=ax^2+bx+c$ avec$a\neq 0$ sont les valeurs de $x$ annulant $P$
c'est à dire telles que $P(x)=0$.
$\Delta=b^2-4ac$
Si $\Delta>0$ donc il y a deux racine $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}$
Si $\Delta=0$ il y a une racine (double) $x_1=\dfrac{-b}{2a}$
Si $\Delta<0$ il n'y a aucune racine
Remarque: Graphiquement, les racines sont les abscisses des points d'intersection de la parabole et de l'axe des abscisses.Aide
Il faut calculer le discriminant $\Delta$
aux signes $-$ dans les calculsSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En utilisant le résultat précédent, résoudre l'inéquation $\dfrac{x^2-6x+5}{3-x}\leq 0$
Aide
Il faut faire le tableau de signes du quotient
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
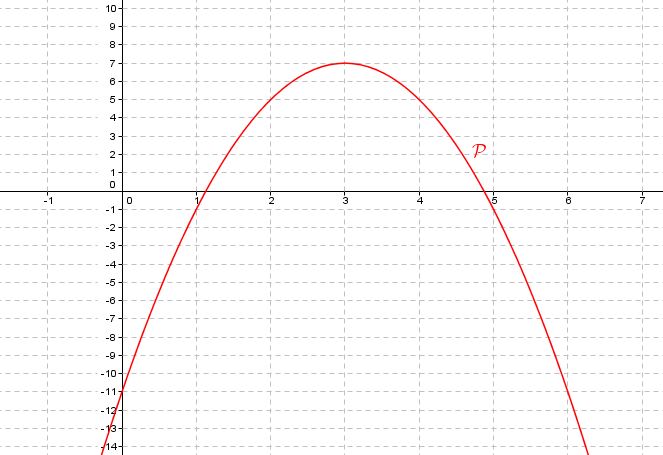
- A l'aide du graphique, déterminer les coefficients $a$, $b$ et $c$ de $f$ tels que $f(x)=ax^2+bx+c$ (On pourra d'abord chercher la forme canonique).
Rappel cours
On peut utiliser les coordonnées du sommet de la parabole pour déterminer la forme canonique
Pour déterminer le coefficient $a$, on peut utiliser le fait que la parabole passe par le point de coordonnées $(0;-11)$ donc on a $f(0)=-11$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - On donne $f(x)=-2x^2+12x-11$.
Résoudre l'inéquation $f(x)\geq 5$.
Expliquer comment contrôler graphiquement le résultat obtenu?Aide
Il faut se ramener à une inéquation de la forme $ax^2+bx+c\geq 0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=-0,005x^2+0,6x-10$.
- Dresser le tableau de variations de $f$.
Rappel cours
Variations fonction polynôme du second degré
Soit la fonction $P$ définie sur $\mathbb{R}$ par sa forme canonique $P (x) = a(x-\alpha)^2 + \beta$
La courbe représentative de $P$ est une parabole dont le sommet a pour coordonnées $(\alpha; \beta)$.
Tableau de variation: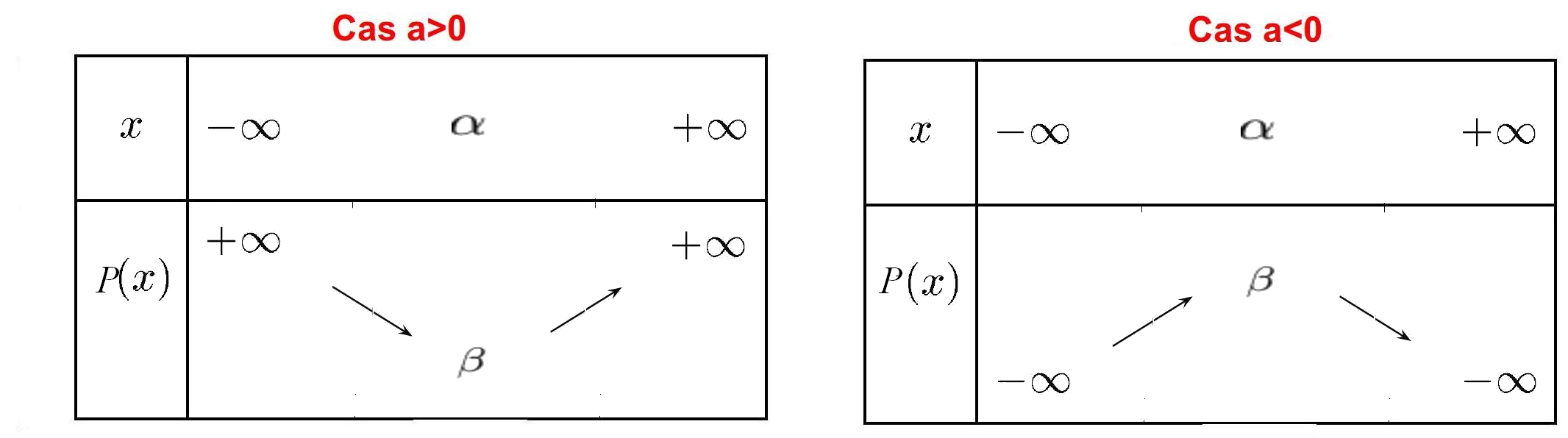
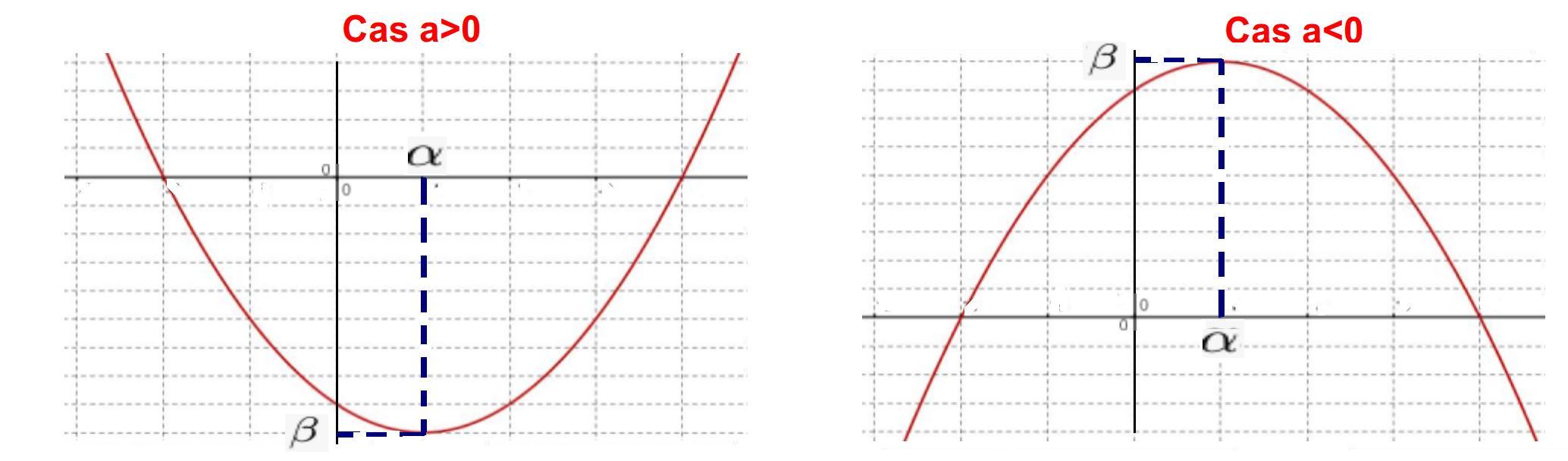
Aide
On peut chercher les coordonnées du sommet de la parabole pour déterminer la forme canonique
Le sens de variation de $f$ dépend du signe du coefficient $a$ de $x^2$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Résoudre l'inéquation $f(x)\geq 0$.
Rappel cours
Signe de $ax^2+bx+c$
- Cas $\Delta>0$ (deux racines $x_1$ et $x_2$

- Cas $\Delta=0$ (une racine $x_1$)

- Cas $\Delta<0$ (aucune racine)

Aide
Il faut chercher les racines de $f(x)=-0,005x^2+0,6x-10$ pour faire le tableau de signes
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Partie B
Une entreprise fabrique et vend des ordinateurs portables.
Le coût de fabrication de $x$ ordinateurs est donné par la fonction $C$ définie par $C(x)=0,005x^2+0,4x+10$, ce coût est exprimé en milliers d'euros.
L'entreprise produit entre 0 et 200 ordinateurs par jour et chaque ordinateur est vendu 1000 euros.
On suppose que toute la production est vendue.
- On note $R(x)$ la recette, en milliers d'euros, engendrée par la vente de $x$ ordinateurs.
Exprimer $R(x)$ en fonction de $x$.Aide
Chaque machine est vendue 1 000 euros soit 1 millier d'euros.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Montrer que le bénéfice, en milliers d'euros, est donné par la fonction $B$ définie sur $[0;200]$ par
$B(x)=f(x)=-0,005x^2+0,6x-10$.Aide
Le bénéfice est égal à la recette diminuée du coût de fabrication.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En utilisant les résultats de la partie A, répondre aux questions suivantes:
- déterminer le bénéfice maximum de l'entreprise.
- déterminer la quantité d'ordinateurs à fabriquer pour que l'entreprise fasse du bénéficeAide
0 On veut déterminer le maximum de la fonction $f$ (voir tableau de variations)
On veut $B(x)\geq 0$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message