Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Déterminer f à partir de la parabole (forme canonique ou factorisée)
Inéquations du second degré
Équation de degré 3
Problème de bénéfice: étude d’une fonction polynôme de degré 2 et recherche du maximum
Ressources associées et exercices semblables
Devoir complet fin de chapitre second degré niveau3 (réf 0516)
devoir
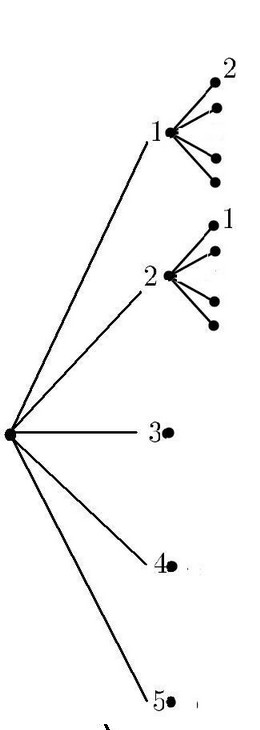
- Déterminer à l'aide du graphique les coordonnées du sommet $S$ de la parabole $C_f$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire la forme canonique de $f$ en utilisant la question 1 et le point $A$ de la courbe $C_f$.
Rappel cours
Forme canonique
Toute fonction polynôme de degré 2 définie sur $\mathbb{R}$ par $P (x) = ax^2 + bx + c$ peut s'écrire sous la forme $P (x) = a(x -\alpha)^2 + \beta$ avec $\alpha=\dfrac{-b}{2a}$ et $\beta= P ( \alpha)$.
Cette écriture de $P (x)$ est appelée forme canonique et $S(\alpha;\beta)$ est le sommet de la parabole représentant la fonction $P$Aide
On a $f(x)=a(x-x_S)+y_S$ et $A(2;-4)$ donc $f(2)=-4$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer graphiquement les solutions de l'équation $g(x)=0$
Aide
Graphiquement, les solutions de l'équation $g(x)=0$ sont les abscisses des points d'intersection de la courbe de de l'axe des abscisses.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire la forme factorisée de $g$ en utilisant la question 3 et le point $B$ de la courbe $C_g$.
Rappel cours
Forme factorisée
- Si le polynôme du second degré $P(x)=ax^2+bx+c$ (avec $a\neq 0$) admet deux racines $x_1$ et $x_2$
alors la forme factorisée de $P$ est $P(x)=a(x-x_1)(x-x_2)$
- Si le polynôme du second degré $P(x)=ax^2+bx+c$ (avec $a\neq 0$) admet une racine $x_1$
alors la forme factorisée de $P$ est $P(x)=a(x-x_1)^2$
- Si le polynôme du second degré $P(x)=ax^2+bx+c$ (avec $a\neq 0$) n'admet aucune racine
alors la forme factorisée de $P$ n'existe pasAide
On a $g(x)=a(x-x_1)(x-x_2)$ et $B(0;6)$ appartient à la courbe $C_g$ donc $g(0)=6$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Donner la forme développée des fonctions $f$ et $g$.
Rappel cours
Identités remarquables
$(a+b)^2=a^2+2ab+b^2$
$(a-b)^2=a^2-2ab+b^2$
$(a-b)(a+b)=a^2-b^2$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Résoudre l'équation $2x^2-4x-4=-x^2-5x+6$
Comment peut-on contrôler les solutions obtenues sur le graphique?Rappel cours
Racines
Les racines de $p(x)=ax^2+bx+c$ avec$a\neq 0$ sont les valeurs de $x$ annulant $P$
c'est à dire telles que $P(x)=0$.
$\Delta=b^2-4ac$
Si $\Delta>0$ donc il y a deux racine $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}$
Si $\Delta=0$ il y a une racine (double) $x_1=\dfrac{-b}{2a}$
Si $\Delta<0$ il n'y a aucune racine
Remarque: Graphiquement, les racines sont les abscisses des points d'intersection de la parabole et de l'axe des abscisses. include126fcludAide
Se ramener à une équation de la forme $ax^2+bx+c=0$ en "passant" tous les termes dans le membre de gauche
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire, à l'aide du graphique, l'ensemble de solution de l'inéquation $f(x) < g(x)$.
Aide
Les solutions sont les abscisses des points de $C_f$ situés strictement en dessous de $C_g$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- $-2x^2+5x-3>0$
Rappel cours
Signe de $ax^2+bx+c$
- Cas $\Delta>0$ (deux racines $x_1$ et $x_2$

- Cas $\Delta=0$ (une racine $x_1$)
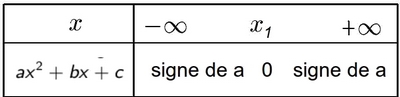
- Cas $\Delta<0$ (aucune racine)
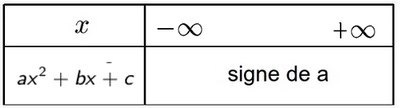
Aide
Chercher les racines de $-2x^2+5x-3$.
Dresser le tableau de signes de $-2x^2+5x-3$.
Ecrire l'ensemble de solution.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $\dfrac{2x^2-5x+2}{x-3}\geq 0$
Aide
Chercher avant tout la valeur interdite
Déterminer les racines de $2x^2-5x+2$
Construire un tableau de signes avec le numérateur $2x^2-5x+2$ et le dénominateur $x-3$
ne pas oublier la double barreSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Montrer que pour tout réel $x$, on a $P(x)=(x-2)(2x^2+x+5)$.
Aide
Développer l'expression $(x-2)(2x^2+x+5)$ et vérifier que cela est égal à $P(x)$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire les solutions de l'équation $P(x)=0$.
Aide
$P(x)=0 \Longleftrightarrow x-2=0$ ou bien $2x^2+x+5$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Le prix de vente unitaire d'un appareil est de 90 euros.
On suppose que tout appareil produit est vendu.
- Exprimer en fonction de $x$ la recette totale.
Aide
La recette correspond à la somme obtenue en vendant $x$ appareils au prix unitaire de 90 euros.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire que le bénéfice horaire réalisé par la fabrication et vente de ces $x$ appareils est donné par la fonction $B$ définie par $B(x)=-x^2+40x-76$.
Aide
Le bénéfice correspond à la recette diminuée des coûts de production.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Dresser le tableau de variation de la fonction $B$ et en déduire le nombre d'appareils à produire pour que le bénéfice horaire soit maximum.
Rappel cours
Signe de $ax^2+bx+c$
- Cas $\Delta>0$ (deux racines $x_1$ et $x_2$

- Cas $\Delta=0$ (une racine $x_1$)

- Cas $\Delta<0$ (aucune racine)

Aide
Chercher les coordonnées du sommet de la parabole représentatnt la fonction bénéfice.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Dresser le tableau de signes de $-x^2+40x-76$.
On donne les racines $x_1=2$ et $x_2=38$ de $-x^2+40x-76$.
L'entreprise réalise-t-elle toujours des bénéfices? Justifier.Aide
Dresser le tableau de signes de $-x^2+40x-76$.
L'entreprise n'est pas en déficit si $B(x)\geq 0$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message