Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Équations menant au second degré
Inéquations menant au second degré
Tableau de signes d’un polynôme de degré 2
Factorisation d’un polynôme de degré 3 et équation de degré 3
Équation avec des coefficients dépendant d’un paramètre
Trajectoire d’un javelot et polynôme de degré 2
Ressources associées et exercices semblables
- $\dfrac{2x^2-10x-5}{x+2} = x-3$
Rappel cours
Racines
Les racines de $p(x)=ax^2+bx+c$ avec$a\neq 0$ sont les valeurs de $x$ annulant $P$
c'est à dire telles que $P(x)=0$.
$\Delta=b^2-4ac$
Si $\Delta>0$ donc il y a deux racine $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}$
Si $\Delta=0$ il y a une racine (double) $x_1=\dfrac{-b}{2a}$
Si $\Delta<0$ il n'y a aucune racine
Remarque: Graphiquement, les racines sont les abscisses des points d'intersection de la parabole et de l'axe des abscisses.Aide
rechercher d'abord la valeur interdite
Les produits en croix sont égaux
Il faut se ramener à une équation de la forme $ax^2+bx+c=0$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $x^4-6x^2+8=0$
Aide
On peut poser $X=x^2$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $1020x^2+x-1021=0$
Rappel cours
Somme et produit des racines
Si le polynôme $P(x)=ax^2+bx+c$ (avec $a\neq 0$) admet deux racines $x_1$ et $x_2$ alors on a:
$ x_1+x_2=\dfrac{-b}{a}$ (somme des racines)
et $x_1x_2=\dfrac{c}{a}$ (produit des racines)Aide
On peut remarquer que 1 est une racine du polynôme
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- $-2x^2+5x-3>0$
Rappel cours
Signe de $ax^2+bx+c$
- Cas $\Delta>0$ (deux racines $x_1$ et $x_2$

- Cas $\Delta=0$ (une racine $x_1$)
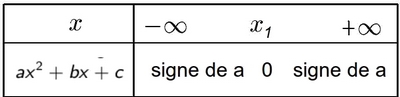
- Cas $\Delta<0$ (aucune racine)
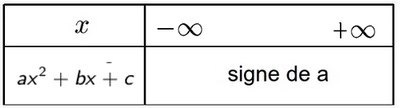
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $ \frac{2x^2-5x+1}{3-x}\leqslant 2$
Aide
il faut chercher les valeurs interdites
puis passer se ramener à une étude de signe du quotient en passant 2 à gaucheSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Montrer que 2 est une solution de cette équation.
Aide
Il faut vérifier que $P(2)=0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer alors les réels $a$, $b$ et $c$ tels que : $P(x)=(x-2)(ax^2+bx+c)$.
Aide
Il faut développer $P(x)=(x-2)(ax^2+bx+c)$ et identifier les coefficients
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire les solutions de l'équation $P(x)=0$.
Rappel cours
Racines
Les racines de $p(x)=ax^2+bx+c$ avec$a\neq 0$ sont les valeurs de $x$ annulant $P$
c'est à dire telles que $P(x)=0$.
$\Delta=b^2-4ac$
Si $\Delta>0$ donc il y a deux racine $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}$
Si $\Delta=0$ il y a une racine (double) $x_1=\dfrac{-b}{2a}$
Si $\Delta<0$ il n'y a aucune racine
Remarque: Graphiquement, les racines sont les abscisses des points d'intersection de la parabole et de l'axe des abscisses.Aide
Il faut chercher les racines du facteur de degré 2
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Résoudre l'inéquation $m^2+5m+4>0$ d'inconnue $m$.
Rappel cours
Signe de $ax^2+bx+c$
- Cas $\Delta>0$ (deux racines $x_1$ et $x_2$

- Cas $\Delta=0$ (une racine $x_1$)

- Cas $\Delta<0$ (aucune racine)

Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire les valeurs de $m$ pour lesquelles l'équation $4mx^2+4(m+2)x-1=0$ admet deux solutions distinctes.
Aide
Il faut que le discriminant soit strictement positif
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
On rappelle que dans un repère orthonormé, $AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$ avec $A(x_A;y;A)$ et $B(x_B;y_B)$.
- Montrer que les coordonnées d'un points $M(x;y)$ appartenant au cercle $\mathcal{C}$ doivent vérifier l'égalité $x^2-8x+y^2-4y+12=0$.
Rappel cours
Distance dans un repère
Dans un repère orthonormé du plan, on a $A(x_A;y_A)$ et $B(x_B;y_B)$,
$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$
Si $\overrightarrow{u}(x;y)$ alors $||\overrightarrow{u}||=\sqrt{x^2+y^2}$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire les coordonnées des points d'intersection du cercle $\mathcal{C}$ avec les axes du repères (axe des abscisses et axe des ordonnées).
On pourra faire une figure pour contrôler graphiquement les résultats obtenus.
Aide
1 Il faut avoir $x=0$ puis $y=0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
La trajectoire de ces billes et un arc de parabole(voir schéma ci-dessous) où $A$ est le point de lancement et $S$ le sommet de l'arc de parabole.
Lors de son lancer, Pierre envoie la bille pour laquelle la hauteur maximale atteinte est de 4,9 m et retombant sur le sol à 14 mètres du point de lancement.
On place une cible circulaire de diamètre 25cm à 10 mètres de la catapulte(point P) dont le centre est à une hauteur $h=3,9$ mètres.
La bille de Pierre traversera-t-elle la cible?
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message