Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Se repérer sur le cercle trigonométrique
Mesure principale
Cos et sin des angles associés
Équations trigonométriques
Ressources associées et exercices semblables
Devoir trigonométrie (réf 0750)
devoir
Devoir équations trigonométriques et fonctions trigonométriques (réf 0751)
devoir
Fiche méthode déterminer la mesure principale d’un angle (réf 0752)
méthode
Fiche méthode résolution d’équations trigonométriques (réf 0754)
méthode
- $\dfrac{-11\pi}{3}$
Rappel cours
Mesure principale
La mesure principale d'un angle est la mesure appartenant à $]-\pi;\pi]$Aide
Calculer $-11\div 3$ et arrondir à l'entier $k$ le plus proche
Il faut ensuite effectuer le calcul $\dfrac{-11\pi}{3}-k\pi$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $\dfrac{33\pi}{9}$
Aide
Calculer $33\div 9$ et arrondir à l'entier $k$ le plus proche
Il faut ensuite effectuer le calcul $\dfrac{33\pi}{9}-k\pi$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $\dfrac{-17\pi}{6}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $\dfrac{-75\pi}{8}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Points sur le cercle trigonométrique:
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- $A = cos(x-\pi)-sin(\pi -x)+cos(\pi +x)-sin(-x)$
Rappel cours
Angles associés
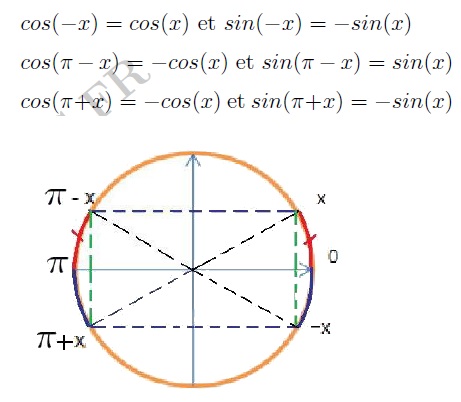
Aide
Exprimer les différents termes en fonction de $cos(x)$ et $sin(x)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $B = sin x+cos(x+\dfrac{\pi}{2})+cos x-sin(x+\dfrac{\pi}{2})$\par
Rappel cours
$cos\left(x-\dfrac{\pi}{2}\right)=sin(x)$ et $cos\left(x+\dfrac{\pi}{2}\right)=-sin(x)$
$sin\left(x-\dfrac{\pi}{2}\right)=sin\left(x+\dfrac{\pi}{2}\right)=cos(x)$Aide
Exprimer les différents termes en fonction de $cos(x)$ et $sin(x)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $C = sin \dfrac{3\pi}{8}+sin \dfrac{5\pi}{8}+sin \dfrac{11\pi}{8}+sin \dfrac{13\pi}{8}$
Aide
$\pi-\dfrac{3\pi}{8}=\dfrac{8\pi}{8}-\dfrac{3\pi}{8}=\dfrac{5\pi}{8}$
De même $\pi+\dfrac{3\pi}{8}=\dfrac{8\pi}{8}+\dfrac{3\pi}{8}=\dfrac{11\pi}{8}$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $D = cos \dfrac{\pi}{10}+cos \dfrac{2\pi}{5}+cos \dfrac{3\pi}{5}+cos \dfrac{9\pi}{10}$
Aide
$\pi-\dfrac{\pi}{10}=\dfrac{10\pi}{10}-\dfrac{\pi}{10}=\dfrac{9\pi}{10}$
De même $\pi-\dfrac{2\pi}{5}=\dfrac{5\pi}{5}+\dfrac{2\pi}{5}=\dfrac{3\pi}{5}$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Calculer les expressions suivantes en utilisant les angles associés :
- Sur $[0;3\pi[$ : $cos x=\dfrac{1}{2}$
Rappel cours
Valeurs remarquables du cos et du sin
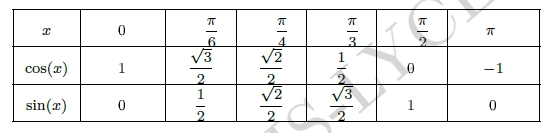
Aide
Déterminer une mesure $\alpha$ telle que $cos(\alpha)=\dfrac{1}{2}$
Rappel: Pour tout réel $x$, $cos(x)=cos(-x)$
$cos(x)=cos(\alpha)\Longleftrightarrow x=\alpha+k2\pi$ ou $ x=-\alpha+k2\pi$ avec $k\in\mtahbb{Z}$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Sur $]-\pi;\pi]$ : $sin x=-\dfrac{\sqrt{2}}{2}$
Aide
Déterminer une mesure $\alpha$ telle que $sin(\alpha)=\dfrac{\sqrt {2}}{2}$
Rappel: Pour tout réel $x$, $sin(x)=sin(\pi-x)$
$sin(x)=sin(\alpha)\Longleftrightarrow x=\alpha+k2\pi$ ou $ x=\pi-\alpha+k2\pi$ avec $k\in\mtahbb{Z}$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Sur $[0;4\pi[$ : $cos x=cos \dfrac{2\pi}{3}$
Aide
Rappel: Pour tout réel $x$, $cos(x)=cos(-x)$
$cos(x)=cos(\alpha)\Longleftrightarrow x=\alpha+k2\pi$ ou $ x=-\alpha+k2\pi$ avec $k\in\mtahbb{Z}$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Sur $[0;2\pi[$ : $cos^2 x =\dfrac{3}{4}$
Aide
Il y a deux possibilités pour $cos(x)$, $\dfrac{\sqrt{3}}{2}$ ou bien $-\dfrac{\sqrt{3}}{2}$
$cos(x)=cos(\alpha)\Longleftrightarrow x=\alpha+k2\pi$ ou $ x=-\alpha+k2\pi$ avec $k\in\mtahbb{Z}$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Sur $]-\pi;\pi]$ : $6-12cos x >0$
Aide
isoler $cos(x)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Sur $]-\pi;2\pi]$ : $sin x\leqslant \dfrac{\sqrt{3}}{2}$
Aide
Résoudre d'abord $sin(x)=\dfrac{\sqrt{3}}{2}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Sur $]-\pi;\pi]$ : $2sin^2 x-sin x -1 = 0$
Aide
On pose $X=sin(x)$
Résoudre ensuite l'équation $2X^2-X-1=0$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Sur $]-\pi;\pi]$ : $sin 2x=sin \dfrac{\pi}{4}$
Aide
résoudre sur $\mathbb{R}$
Déterminer les valeurs de $x$ dans $]-\pi;\pi]$ en prenant $k=0$, $k=1$, $k=-1$, $k=2$.....Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message