Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Coefficients avec un paramètre m
Calcul du discriminant
Signe d’un polynôme de degré 2
Ressources associées et exercices semblables
- Pour quelles valeurs de $m$ la courbe représentative de $f$ est-elle une parabole?
Aide
Pour que la représentation graphique de $f$ soit une parabole, il faut que $f_m$ soit une fonction polynôme de degré 2
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Exprimer le discriminant en fonction de $m$.
Rappel cours
Discriminant
$P(x)=ax^2+bx+c$ avec $a\neq 0$.
Le discriminant du polynôme du second degré $P$ est $\Delta=b^2-4ac$Aide
On a ici $a=m+1$, $b=2$ et $c=m$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer les valeurs de $m$ pour lesquelles on a $f(x)<0$ pour tout réel $x$.
Rappel cours
Signe de $ax^2+bx+c$
- Cas $\Delta>0$ (deux racines $x_1$ et $x_2$

- Cas $\Delta=0$ (une racine $x_1$)
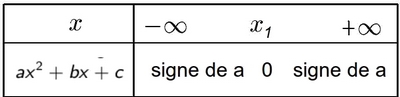
- Cas $\Delta<0$ (aucune racine)
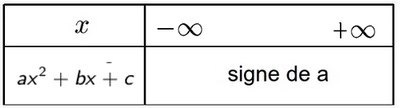
Aide
$f_m(x)<0$ s'il n'y a aucune racine et $f_m(x)$ est alors de signe constant et est du même signe que le coefficient de $x^2$ qui est ici $m+1$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements Un polynôme est de signe constant s'il n'admet aucune racine .
donc $f_m(x)<0$ si $\Delta < 0$ et alors $f_m(x)$ est du même signe que le coefficient $m+1$ de $x^2$.
On doit donc avoir dans un premier temps $\Delta<0$.
Etude du signe de $\Delta=4(-m^2-m+1)$ ou bien de $-m^2-m+1$:
$\Delta_1=b^2-4ac=(-1)^2-4\times (-1)\times 1=5$
$\Delta_1>0$ donc il y a deux racines
$m_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{1 +\sqrt{5} }{-2 }=\dfrac{-1-\sqrt{5}}{2}$
et $m_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{ 1 -\sqrt{5} }{-2 }=\dfrac{-1+\sqrt{5}}{2}$

On veut $\Delta_1 <0$
donc $f_m(x)$ n'admet aucune racine pour $m < \dfrac{-1-\sqrt{5}}{2}$ et pour $m > \dfrac{-1+\sqrt{5}}{2}$
$f_m(x)$ est donc du signe du coefficient $m+1$ de $x^2$ donc pour avoir $f_m(x)<0$ il faut $m+1 <0$ soit $m < -1$.
On doit donc avoir $m\in \left] -\infty;\dfrac{-1-\sqrt{5}}{2}\right[\cup \left]\dfrac{-1+\sqrt{5}}{2};+\infty\right[$ et aussi $m < -1$


 Envoyez votre message
Envoyez votre message