Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Équations trigonométriques avec cosinus et sinus
Mesure principale des solutions et sur $[0;2\pi]$
Ressources associées et exercices semblables
Équations de base avec sinus (réf 0726)
exercice
Équations avec cosinus (réf 0727)
exercice
Équations avec sinus (réf 0728)
exercice
Fiche méthode résolution d’équations trigonométriques (réf 0754)
méthode
On pourra utiliser le cercle trigonométrique.
- $cos(x)=cos(\dfrac{\pi}{7})$
Aide
il y a deux valeurs possibles donnant le même cosinus
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $sin(x)=sin(\dfrac{\pi}{5})$
Rappel cours
Cosinus et sinus d'un nombre réel
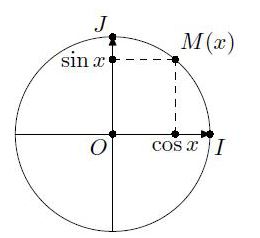
Soit $(O;I,J)$ un repère orthonormé et $\mathcal{C}$ le cercle trigonométrique. Soit $x$ un réel et $M$ le point correspondant sur le cercle.
On appelle cosinus de $x$ et on note $cos(x)$ l'abscisse du point $M$.
On appelle sinus de $x$ et on note $sin(x)$ l'ordonnée du point $M$.
Aide
il y a deux points sur le cercle donnant le même sinus
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $sin(x)=\dfrac{-\sqrt{2}}{2}$
Rappel cours
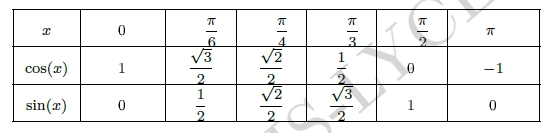
Valeurs remarquables du cos et du sin
Aide
$sin\left(\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}$
donc $sin\left(-\dfrac{\pi}{4}\right)=\dfrac{-\sqrt{2}}{2}$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements