Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Équations se ramenant à cos(x)=k
Résolution d¡équations trigonométriques dans R
Ressources associées et exercices semblables
Équations de base avec sinus (réf 0726)
exercice
Équations trigonométriques (réf 0729)
exercice
Fiche méthode résolution d’équations trigonométriques (réf 0754)
méthode
On pourra utiliser le cercle trigonométrique.
- $2cos(x)=-1$
Rappel cours
Valeurs remarquables du cos et du sin
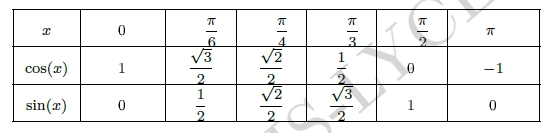
Aide
Isoler $cos(x)$
Chercher une valeur de $\alpha$ telle que $cos(\alpha)=\dfrac{1}{2}$.
Utiliser le cercle trigonométrique et les symétries par rapport aux axes du repère et par rapport à l'origine pour déterminer les valeurs de $x$
il y a deux valeurs de $x$ donnant le même cosinusSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $2cos(x)+1=2$
Aide
Isoler $cos(x)$
Chercher une mesure $\alpha$ telle que $cos(\alpha)=\dfrac{1}{2}$
En déduire les valeurs pour lesquelles $cos(x)=\dfrac{1}{2}$
il y a deux valeurs de $x$ donnant le même cosinusSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $cos(x)=\dfrac{-1}{\sqrt{2}}$
Aide
Ecrire le membre de gauche sans racine carrée au dénominateur
Chercher une mesure $\alpha$ telle que $cos(\alpha)=\dfrac{\sqrt{2}}{2}$
Utiliser le cercle trigonométrique et les symétries par rapport aux axes du repère et par rapport à l'origine pour déterminer les valeurs de $x$
il y a deux valeurs de $x$ donnant le même cosinusSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements