Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Dérivée avec exponentielle et formules de dérivation
Tableau de variation
Position d’une courbe par rapport à une droite
Ressources associées et exercices semblables
On note $C_f$ sa représentation graphique dans un repère orthogonal.
- Calculer la dérivée de $f$ et dresser son tableau de variation.
Rappel cours
Dérivée de $exp(x)$ et de $exp(kx)$
La fonction $exp$ est dérivable sur $\mathbb{R}$ et $(exp(x))'=exp(x)$
La fonction $f$ définie par $f(x)=exp(kx)=e^{kx}$ avec $k$ réel est dérivable sur $\mathbb{R}$ et $f'(x)=kexp(kx)=ke^{kx}$
Égalité et inégalités avec exponentielle
Pour tous réels $a$ et $b$, on a:
$e^a=e^b\Longleftrightarrow a=b$
$e^a < e^b\Longleftrightarrow a < b$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - On donne ci-dessous la représentations graphique $C_h$ et $C_g$ de la fonction $h$ définie sur $\mathbb{R}$ par $h(x)=e^x$.
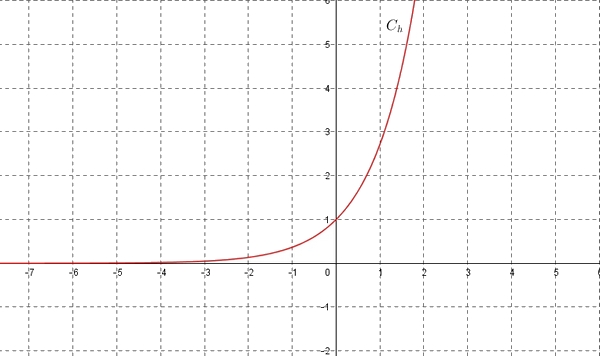
Dans le même repère, tracer la représentation graphique de la fonction $g$ définie sur $\mathbb{R}$ par $g(x)=x-1$.
En utilisant le graphique, comparer $h(x)$ et $g(x)$.Aide
$g$ est une fonction affine
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Vérifier la conjecture faite à la question 2.
Aide
Pour comparer $h(x)$ et $g(x)$, on peut pétudier le signe de $g(x)-h(x)$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION