Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Se ramener à une inéquation du second degré
Tableau de signes d’un polynôme de degré 2
Ressources associées et exercices semblables
Tableau de signes d’un polynôme de degré 2 (réf 0479)
exercice
Vidéo de l’exercice
Rappel cours
Signe de $ax^2+bx+c$
- Cas $\Delta>0$ (deux racines $x_1$ et $x_2$

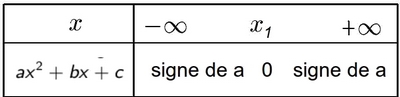
- Cas $\Delta=0$ (une racine $x_1$)
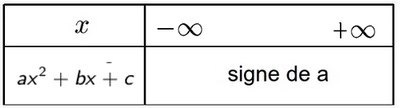
- Cas $\Delta<0$ (aucune racine)
Aide
Se ramener à une inéquation de la forme $ax^2+bx+c\leq 0$
Rechercher les racines du polynôme $ax^2+bx+c$
Dresser le tableau de signes de $ax^2+bx+c$
Donner l'ensemble de solution
Solution
$3x^2+4x-5\leq -x-3 $
$\Longleftrightarrow 3x^2+4x-5+x+3\leq 0$
$ \Longleftrightarrow 3x^2+5x-2\leq 0$
Recherche des racines de $3x^2+5x-2$
$\Delta=b^2-4ac$
$~~~~~=5^2-4\times 3\times (-2)$
$~~~~=25+24=49$
$\Delta>0$ donc il y a deux racines:
$\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-5-7}{6}=-2$ et
$x_2=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-5+7}{6}=\dfrac{1}{3}$
Tableau de signes

Ensemble de solutions
On veut que $3x^2+5x-2$ soit de signe négatif ($-$) ou nul(zone rouge du tableau)

Donc $x$ appartient à la zone verte du tableau


 Envoyez votre message
Envoyez votre message