Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Inéquation du second degré avec un quotient
Ressources associées et exercices semblables
Intersection d’une droite et d’une hyperbole (réf 0502)
exercice
Intersection d’une droite et d’une parabole (réf 0503)
exercice
Vidéo de l’exercice
On note respectivement $C_f$ et $C_g$ les représentations graphiques de $f$ et $g$ dans un repère orthogonal
- En utilisant la calculatrice ou GEOGEBRA, conjecturer la position relative de $C_:f$ et $C_g$.
Aide
La position relative de $C_F$ et $C_g$ consiste à déterminer les valeurs de $x$ pour lesquelles la courbe $C_f$ est au-dessus de $C_g$ par exemple
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Prouver que cette conjecture est correcte par le calcul.
Rappel cours
Racines
Les racines de $p(x)=ax^2+bx+c$ avec$a\neq 0$ sont les valeurs de $x$ annulant $P$
c'est à dire telles que $P(x)=0$.
$\Delta=b^2-4ac$
Si $\Delta>0$ donc il y a deux racine $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}$
Si $\Delta=0$ il y a une racine (double) $x_1=\dfrac{-b}{2a}$
Si $\Delta<0$ il n'y a aucune racine
Remarque: Graphiquement, les racines sont les abscisses des points d'intersection de la parabole et de l'axe des abscisses. Signe de $ax^2+bx+c$
- Cas $\Delta>0$ (deux racines $x_1$ et $x_2$

- Cas $\Delta=0$ (une racine $x_1$)
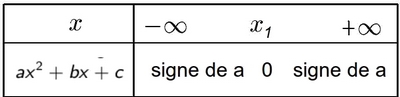
- Cas $\Delta<0$ (aucune racine)
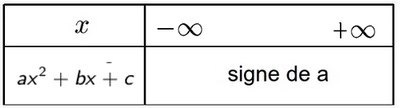
Aide
Il faut résoudre l'inéquation $f(x)>g(x)$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION


 Envoyez votre message
Envoyez votre message