Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Calcul d’un bénéfice
Forme canonique et maximum de la fonction polynôme de degré 2
Racines et bénéfice positif
Ressources associées et exercices semblables
Trajectoire d’un ballon de basket (réf 0499)
exercice
Recettes, coûts et recherche d’un bénéfice maximum (réf 0500)
exercice
Le coût total de fabrication de $q$ appareils est $C(q)=50q-q^2+20$.
Le coût est exprimé milliers d'euros avec $q\in[0;50]$.
On admet que chaque appareil fabriqué est vendu au prix unitaire de 10500 euros et que toute la production est vendue.
La figure ci-dessous, donne la courbe représentative de la fonction coût total dans un repère orthogonal.
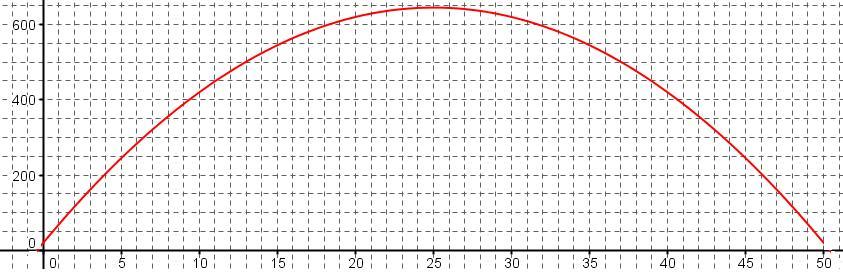
- Déterminer la quantité d'appareils à produire pour que le coût de production soit maximal.
Rappel cours
Forme canonique
Toute fonction polynôme de degré 2 définie sur $\mathbb{R}$ par $P (x) = ax^2 + bx + c$ peut s'écrire sous la forme $P (x) = a(x -\alpha)^2 + \beta$ avec $\alpha=\dfrac{-b}{2a}$ et $\beta= P ( \alpha)$.
Cette écriture de $P (x)$ est appelée forme canonique et $S(\alpha;\beta)$ est le sommet de la parabole représentant la fonction $P$ Variations fonction polynôme du second degré
Soit la fonction $P$ définie sur $\mathbb{R}$ par sa forme canonique $P (x) = a(x-\alpha)^2 + \beta$
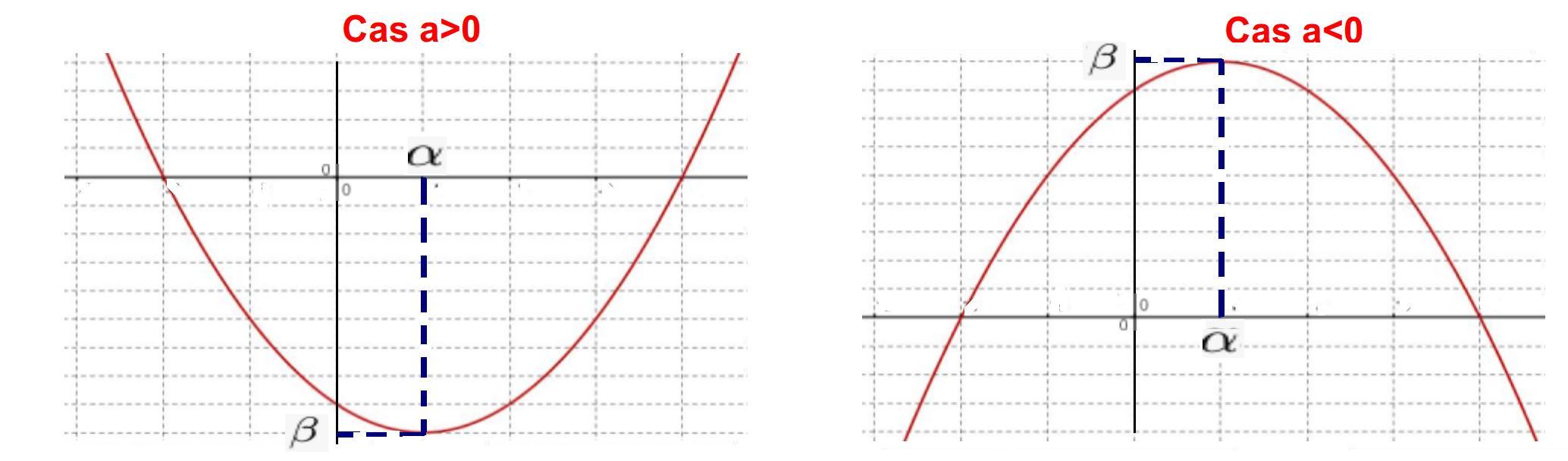
La courbe représentative de $P$ est une parabole dont le sommet a pour coordonnées $(\alpha; \beta)$.
Tableau de variation: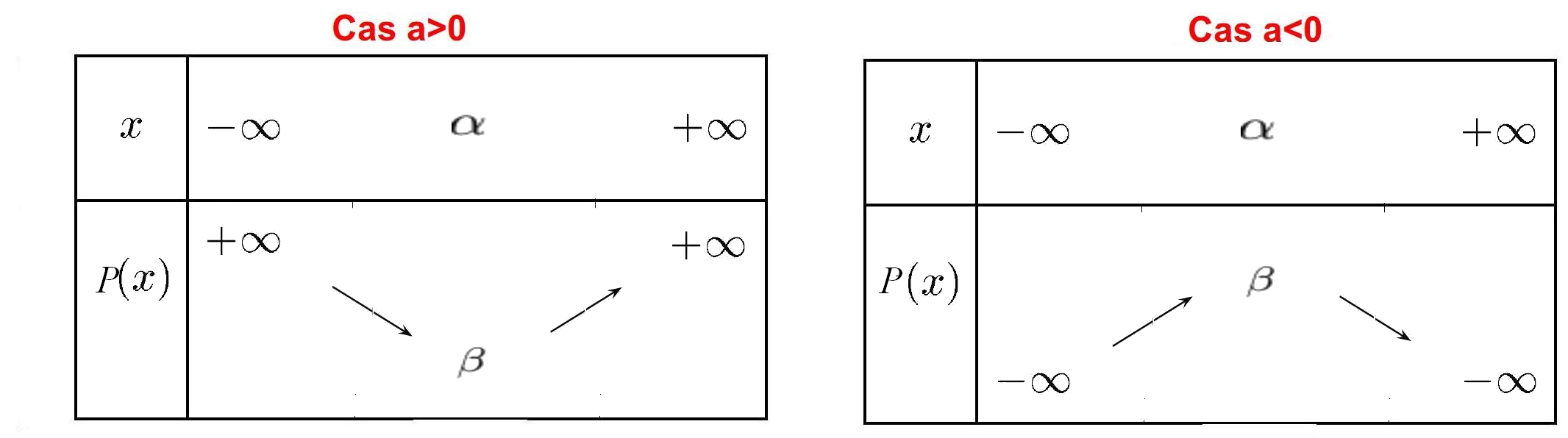
Aide
Il faut déterminer les coordonnées du sommet de la parabole et dresser le tableau de variation de la fonction $C$.
L'expression de $C$ n'est pas ordonnée selon les puissances décroissante de $q$.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Exprimer la recette $R(q)$, en milliers d'euros, en fonction de $q$.
Aide
Si on vend $q$ objets au prix unitaire de $p$ euros, la recette engendrée est de $p\times q$ euros.
es prix sont à utiliser en milliers d'eurosSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Exprimer alors le bénéfice $B(q)$, en milliers d'euros, réalisé par cette entreprise en fonction de $q$.
Aide
Le bénéfice est la différence entre la rcette et le coût total de production
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer alors la quantité à produire pour que l'entreprise ne soit pas en déficit
Rappel cours
Racines
Les racines de $p(x)=ax^2+bx+c$ avec$a\neq 0$ sont les valeurs de $x$ annulant $P$
c'est à dire telles que $P(x)=0$.
$\Delta=b^2-4ac$
Si $\Delta>0$ donc il y a deux racine $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}$
Si $\Delta=0$ il y a une racine (double) $x_1=\dfrac{-b}{2a}$
Si $\Delta<0$ il n'y a aucune racine
Remarque: Graphiquement, les racines sont les abscisses des points d'intersection de la parabole et de l'axe des abscisses.Aide
Il faut déterminer les valeurs de $q$ pouir lesquelles on a un bénéfice positif soit $B(q)>0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Tracer la représentation graphique $C_R$ de la fonction $R$ dans le même repère que la fonction coût de fabrication.
Comment peut-on retrouver graphiquement le résultat de la fonction précédente?Aide
$R$ est une fonction linéaire donc sa représentation graphique est une droite passant par l'origine du repère.
Pour que le bénéfice soit positif, il faut que $R(q)$ soit supérieur à $C(q)$.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message