Envoyez votre messageInformations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Inscrivez vous gratuitement ici....
Contenu
Maximum de la fonction inverse sur un intervalle
Ressources associées et exercices semblables
Calculs d’images et d’antécédents par la fonction inverse (réf 261)
exercice
Comparaison d’images avec la fonction inverse(réf 262)
exercice
Déterminer dans chaque cas le maximum et le minimum de $f$ sur l'intervalle $I$.
- $I=[2;5]$
Rappel cours
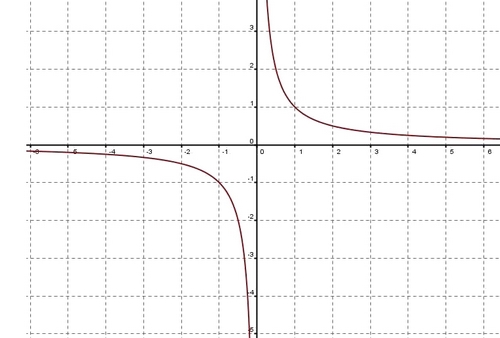
Fonction inverse
La fonction inverse est définie sur $\mathbb{R}^*$ (tous les réels sauf $0$)
et est strictement décroissante sur $]-\infty;[$ et sur $]0;+\infty[$.
La représentation graphique de la fonction inverse est une hyperbole.
Aide
Il faut utiliser les variations de la fonction inverse sur $]0;+\infty[$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $I=[-4;-1]$
Aide
Il faut utiliser les variations de la fonction inverse sur $]-\infty;0[$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $I=\left[\dfrac{1}{4};\dfrac{1}{2}\right]$
Aide
Il faut utiliser les variations de la fonction inverse sur $]0;+\infty[$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements