Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Équations
Factorisation et produit de facteurs nul
Équations et fonction
Ressources associées et exercices semblables
- $(x-1)(x+2)-(x-1)(2x+3)=0$
Rappel cours
Produit de facteurs nul
Un produit de facteurs est nul si l'un des facteurs est nul.
$a \times b=0 \Longleftrightarrow a=0$ ou $b=0$
Aide
Il faut factoriser le membre de gauche
Solution
Vous devez être abonné accéder à ce contenu, à partir de 2 euros par mois...
- $(2x+1)^2=(x+2)(4x+3)$
Rappel cours
Identités remarquables
$(a+b)^2=a^2+2ab+b^2$
$(a-b)^2=a^2-2ab+b^2$
$(a-b)(a+b)=a^2-b^2$
Aide
Ici, on ne peut factoriser (pas de facteur commun) donc on peut développer et simplifier, les termes en $x^2$ "s'éliminent"
Solution
Vous devez être abonné accéder à ce contenu, à partir de 2 euros par mois...
- $\dfrac{3}{x-2}=\dfrac{-2}{x}$
Rappel cours
Quotients égaux
$\dfrac{a}{b}=\dfrac{c}{d} \Longleftrightarrow ac=bd$ (avec $b\neq 0$ et $d\neq 0$)Aide
Penser à chercher d'abord les valeurs interdites pour donner l'ensemble des valeurs de $x$ possibles
Les produits en croix doivent être égauxSolution
Vous devez être abonné accéder à ce contenu, à partir de 2 euros par mois...
- Résoudre l'équation $f(x)=7$
Aide
On peut passer tous les termes dans le membre de gauche et factoriser
Solution
Vous devez être abonné accéder à ce contenu, à partir de 2 euros par mois...
- Résoudre l'équation $f(x)=3$
Rappel cours
Identités remarquables
$(a+b)^2=a^2+2ab+b^2$
$(a-b)^2=a^2-2ab+b^2$
$(a-b)(a+b)=a^2-b^2$
Aide
On peut passer tous les termes dans le membre de gauche et factoriser
Solution
Vous devez être abonné accéder à ce contenu, à partir de 2 euros par mois...
- On donne ci-dessous la représentation graphique de $C_f$.
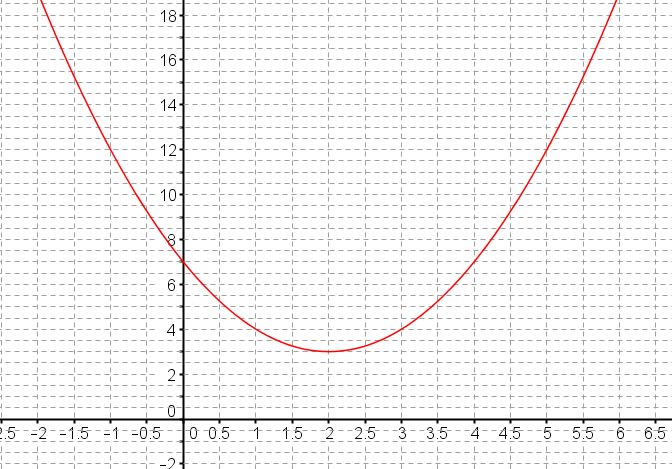
Contrôler graphiquement les résultats de chacune des questions. (on fera apparaître les tracés permettant de contrôler ces résultats.Solution
Vous devez être abonné accéder à ce contenu, à partir de 2 euros par mois...


 Envoyez votre message
Envoyez votre message