Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Intervalle de fluctuation
Probabilités avec un tableau à double entrée
Ressources associées et exercices semblables
Devoir court probabilités, diagramme de Venn et tableau à double entrée (réf 1549)
devoir
On effectue un sondage auprès de 350 personnes, et 182 déclarent avoir l'intention de voter pour ce candidat.
- Déterminer une intervalle de fluctuation au seuil de 95%. On donnera des bornes avec la précision de $10^{-3}$.
Rappel cours
Intervalle de confiance-estimation
On prélève un échantillon de taille $n$ dans une population.
On note $f$ la fréquence du caractère dans l'échantillon prélevé.
On note $p$ la proportion du caractère dans la population totale ($p$ étant inconnue)
Si $0,2\leq f\leq 0,80$et $n\geq 25$ alors dans au moins 95% des cas,
L'intervalle de confiance au seuil de 95% est $I_C=\left[f-\dfrac{1}{\sqrt{n}} ; f+\dfrac{1}{\sqrt{n}}\right]$ .
On peut estimer que $p$ est dans cet intervalle avec un seuil de confiance de 95%.
L'amplitude de cet intervalle (écart entre les deux bornes) est $\dfrac{2}{\sqrt{n}}$Aide
On a ici $f=0,54$ et $n=350$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Le candidat est il-certain d'être élu?
Aide
Pour être élu, il faut au minimum receuillir 50% des votes
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Quel est le nombre minimum de personnes à interroger pour obtenir un intervalle de fluctuation plus précis avec une amplitude inférieure à $0,01$ (soit moins de 1%)
Aide
Rappel, l'amplitude de l'intervalle de fluctuation est $\dfrac{1}{2\sqrt{n}}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- le premier, des bulbes à fleurs rouges dont 90% donnent une fleur,
- le second, des bulbes à fleurs jaunes dont 80% donnent une fleur.
Un horticulteur achète 70% des bulbes qu'il cultive au premier grossiste et le reste au second. Un bulbe donne au plus une fleur. L'horticulteur plante un bulbe au hasard.
On utilisera le notations suivantes: $F$: "le bulbe donne une fleur" et $R$: "la fleur est rouge"
- Décrire l'événement $\overline F$ puis l'événement $\overline R$.
Rappel cours
Notations des événements et probabilités
$\Omega$ est l'événement certain et $p(\Omega)=1$
$\oslash$ est l'événement impossible et $p(\oslash)=0$
$\overline{A}$ est l'événement contraire de A et est composé de toutes les issues de $\Omega$ qui ne sont pas contenue dans A et $p(\overline{A})=1-p(A)$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Compléter le tableau à double entrée suivant en considérant par exemple un ensemble de 100 bulbes:
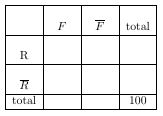 fboc
fbocSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements- En utilisant le tableau, déterminer la probabilité de:
- d'obtenir une fleur rouge ?
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - d'obtenir une fleur jaune ?
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - de ne pas obtenir de fleur ?
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Donner une estimation de la proportion de bulbes donnant une fleur rouge au seuil de confiance de 95% dans l'ensemble de la production.
Rappel cours
Intervalle de confiance-estimation
On prélève un échantillon de taille $n$ dans une population.
On note $f$ la fréquence du caractère dans l'échantillon prélevé.
On note $p$ la proportion du caractère dans la population totale ($p$ étant inconnue)
Si $0,2\leq f\leq 0,80$et $n\geq 25$ alors dans au moins 95% des cas,
L'intervalle de confiance au seuil de 95% est $I_C=\left[f-\dfrac{1}{\sqrt{n}} ; f+\dfrac{1}{\sqrt{n}}\right]$ .
On peut estimer que $p$ est dans cet intervalle avec un seuil de confiance de 95%.
L'amplitude de cet intervalle (écart entre les deux bornes) est $\dfrac{2}{\sqrt{n}}$Aide
penser á vérifier que les conditions d'application pour effectuer les calculs sont satisfaites
Il faut déterminer l'intervalle de fluctuation.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En utilisant le tableau, déterminer la probabilité de:
Infos abonnements


 Envoyez votre message
Envoyez votre message