Devoir matrices, calculs avec les matrices, systèmes d’équations (réf 1642) Chapitre 4 MATRICES, Option maths expertes, séquence 4 exercices de synthèse et devoirs d'entraînement

Home Option maths expertes Chapitre 4 MATRICES séquence 4 exercices de synthèse et devoirs d'entraînement

Devoir matrices, calculs avec les matrices, systèmes d’équations (réf 1642)

Ressource précédente: Devoir matrices et opérations sur les matrices (réf 1640) Ressource suivante: Devoir complet matrices, opérations sur les matrices et systèmes d’équations (réf 1641)

Informations

Vous devez être inscrit pour accéder à ces informations.

Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.

Inscrivez vous gratuitement ici....

Contenu

Coefficients d’une matrice

Produit de deux matrices

Inverse d’une matrice

Systèmes d’équations et matrices

Suites et matrices

Ressources associées et exercices semblables

Devoir matrices et opérations sur les matrices (réf 1640)
devoir

Devoir complet matrices, opérations sur les matrices et systèmes d’équations (réf 1641)
devoir

| | | |

Exercice 1 (2 points)

Écrire une matrice carrée $A$ d'ordre 3 telle que $a_{ij}=1$ si $i=j$ et $a_{ij}=2i-j$ si $i< j$ et $a_{ij}=0$ si $i>j$

Aide

Si $i=j$ alors $a_{i,j}$ est un coefficient de la diagonale
Si $i > j$ alors $a_{i,j}$ est un coefficient en dessous de la diagonale

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements

Exercice 2 (3 points)

On donne $A=\begin{pmatrix} 3&1&3\\ 1&2&2\\ 1&-1&-1 \end{pmatrix}$ $B=\begin{pmatrix} -1 & 1 \\ 1 & 2 \\ 2 & -1 \end{pmatrix}$

Calculer $2A+I_3$

Rappel cours

Matrice identité
La matrice carrée identité d'ordre $n$ notée $I_n$ est la matrice diagonale dont tous les coefficients de la diagonale sont égaux à 1.
Si $A$ est une matrice $n\times p$, on a $AI_p=A$ et $I_nA=A$.
Par exemple $I_2=\begin{pmatrix} 1&0\\0&1 \end{pmatrix}$, $I_3=\begin{pmatrix} 1&0&0\\0&1&0\\0&0&1 \end{pmatrix}$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Le produit $A\times B$ existe t'il ? (justifier à l'aide d'une phrase). Si oui calculer $A\times B$ en détaillant les calculs

Rappel cours

Produit de deux matrices
Le produit de la matrice $A=(a_{ij})$ de dimensions $n\times p$ par la matrice $B=(b_{ij})$ de dimensions $p\times m$ est la matrice $C=(c_{ij})=A\times B$ de dimensions $n\times m$ telle que $c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+...+a_{ip}b_{pj}=\sum_k=1^p a_{ik}b_{kj}$}
Schématiquement on a:

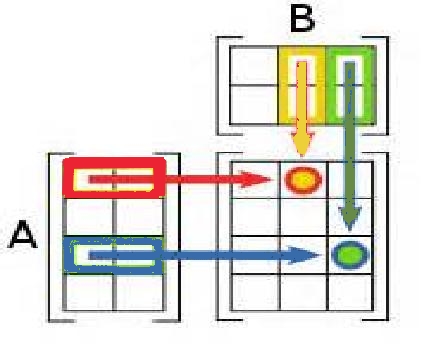
Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Le produit $B\times A$ existe t'il ? (justifier à l'aide d'une phrase). Si oui calculer $B\times A$ en détaillant les calculs

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements

Exercice 3 (5 points)

On donne la matrice $A=\begin{pmatrix} a&5\\ 3&4 \end{pmatrix}$ avec $a$ réel.

Pour quelle valeur de $a$ la matrice $A$ n'est pas inversible?

Rappel cours

Déterminant d'une matrice carrée d'ordre 2
Soit $A=\begin{pmatrix} a&b\\c&d \end{pmatrix}$
le déterminant de $A$ noté $det(A)$ est le réel $det(A)=ad-bc$}

Aide

Il faut déterminer quelle valeur de $a$ annule le déterminant

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Pour la suite, on a $a=4$
Calculer $A^{-1}$

Rappel cours

Inverse d'une matrice carrée d'ordre 2
Soit $A=\begin{pmatrix} a&b\\c&d \end{pmatrix}$ telle que $det(A)\neq 0$.
$A^{-1}=\dfrac{1}{det(A)}\begin{pmatrix} d&-b\\-c&a \end{pmatrix}$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
On considère le système d'équations $\begin{cases}4x+5y=2\\ 3x+4y=1 \end{cases}$
Donner l'écriture matricielle de ce système d'équations.

Rappel cours

Système d'équations et matrices
Un système à $n$ équations et à $n$ inconnues de la forme $\begin{cases} a_{11}x_1+a_{12}x_2+a_{13}x_3+...+a_{1n}x_n=b_1\\ a_{21}x_1+a_{22}x_2+a_{23}x_3+...+a_{2n}x_n=b_2\\ ...\\ ...\\ ...\\ a_{n1}x_1+a_{n2}x_2+a_{n3}x_3+...+a_{nn}x_n=b_n \end{cases} $ peut sécrire sous la forme $AX=B$ avec
$A=\begin{pmatrix} a_{11}&a_{12}&a_{13}&...&a_{1n}\\ a_{21}&a_{22}&a_{23}&...&a_{2n}\\ ...\\ ...\\ ...\\ a_{n1}&a_{n2}&a_{n3}x_3&...&a_{nn} \end{pmatrix}$
$X=\begin{pmatrix} x_1\\x_2\\...\\...\\x_n \end{pmatrix}$ et $B=\begin{pmatrix} b_1\\b_2\\...\\...\\b_n \end{pmatrix}$
Si $A$ est inversible on a alors $AX=B\Longleftrightarrow A^{-1}AX=A^{-1}B\Longleftrightarrow X=A^{-1}B$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
En déduire les solutions de ce système d'équations

Aide

Il faut calculer $A^{-1}\times B$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements

Exercice 4 (3 points)

On considère la matrice $A=\begin{pmatrix} 1&0&2\\0&-1&1\\1&-2&0\end{pmatrix}$
Avec la calculatrice, calculer $A^3-A$ et en déduire que $A$ est inversible.
Exprimer alors $A^{-1}$ en fonction de $A$

Rappel cours

Inverse d'une matrice carrée d'ordre $n$
Soit $A$ une matrice carrée d'ordre $n$, $A$ est un inversible s'il existe une matrice carrée d'ordre $n$ notée $A^{-1}$ telle que $A\times A^{-1}=I_n$

Aide

$A^3-A=A(A^2-I_3)$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements

Exercice 5 (7 points)

On considère les suites $(u_n)$ et $V_n)$ définie pour tout entier naturel $n$ par
$\begin{cases}u_{n+1}=0,9u_n+0,4v_n\\v_{n+1}=0,1u_n+0,6v_n\end{cases}$ et $u_0=0$ et $v_0=1$

On pose $E_n=\begin{pmatrix}u_n\\v_n\end{pmatrix}$
Donner la valeur de $E_0$ puis déterminer la matrice carrée d'ordre 2 $M$ telle que $E_{n+1}=M\times E_n$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Pour la suite On admet que $E_n=M^n\times E_0$
On pose $A=\begin{pmatrix} 0,8&0,8\\0,2&0,2 \end{pmatrix}$ et $B=\begin{pmatrix} 0,2&-0,8\\-0,2&0,8 \end{pmatrix}$
Montrer que $M=A+\dfrac{1}{2}B$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
On admet que $A^2=A$ et $B^2=B$
Vérifier que $AB=BA=\begin{pmatrix} 0&0\\0&0 \end{pmatrix}$
Montrer par récurrence que $M^n=A+0,5^nB$ pour tout entier naturel $n>0$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
En déduire que $u_n=0,8-0,8\times 0,5^n$

Aide

$E_n=M^n\times E_0$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements

Vous devez être abonné pour accéder à ce contenu...

Infos abonnements

Ressource précédente: Devoir matrices et opérations sur les matrices (réf 1640) Ressource suivante: Devoir complet matrices, opérations sur les matrices et systèmes d’équations (réf 1641)