Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Calcul du produit de deux matrices et contrôle avec la calculatrice
Ressources associées et exercices semblables
Produit de deux matrices (réf 1614)
exercice
Puissance d’une matrice (réf 1616)
exercice
Penser à contrôler le résultat avec la calculatrice (voir cours)
- $A=\begin{pmatrix}
2&1\\
4&-1
\end{pmatrix}$ et $B=\begin{pmatrix}
2&3&-1\\
3&-2&4
\end{pmatrix}$.
Rappel cours
Produit de deux matrices
Le produit de la matrice $A=(a_{ij})$ de dimensions $n\times p$ par la matrice $B=(b_{ij})$ de dimensions $p\times m$ est la matrice $C=(c_{ij})=A\times B$ de dimensions $n\times m$ telle que $c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+...+a_{ip}b_{pj}=\sum_k=1^p a_{ik}b_{kj}$}
Schématiquement on a:
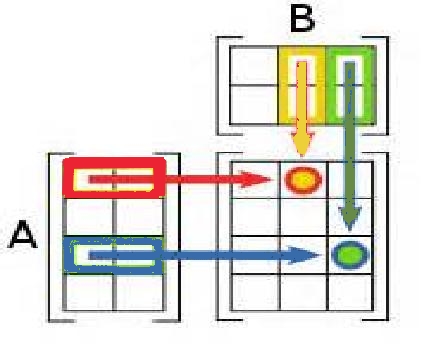
Aide
Il faut que le nombre de colonnes de $A$ soit égal au nombre de lignes de $B$.
On multiplie les coefficients de la première ligne de $A$ par les coefficients de la première colonne de $B$, puis par ceux de la deuxième colonne de $B$......Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $A=\begin{pmatrix}
2&-3\\
1&-5
\end{pmatrix}$ et $B=\begin{pmatrix}
2&-1\\
-2&4
\end{pmatrix}$.
Aide
Il faut que le nombre de colonnes de $A$ soit égal au nombre de lignes de $B$.
On multiplie les coefficients de la première ligne de $A$ par les coefficients de la première colonne de $B$, puis par ceux de la deuxième colonne de $B$......Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $A=\begin{pmatrix}
2&-3&1\\
1&-5&8
\end{pmatrix}$ et $B=\begin{pmatrix}
2&-1&2\\
-2&4&9
\end{pmatrix}$.
Aide
Il faut que le nombre de colonnes de $A$ soit égal au nombre de lignes de $B$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message