Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Condition d’existence du produit de deux matrices
Calcul de A^2 et de A^3
Contrôle avec la calculatrice NumWorks
Ressources associées et exercices semblables
Produit de deux matrices (réf 1614)
exercice
Produit de deux matrices (réf 1615)
exercice
- Soit $A$ une matrice.
Quelle doit-être la caractéristique de $A$ pour que l'on puisse calculer $A^2$?Aide
Pour pouvoir calculer $A\times B$, il faut que le nombre de colonnes de $A$ soit égal au nombre de lignes de $B$
$A^2=A\times A$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Calculer $A^2$ avec $A=\begin{pmatrix}
2&1\\
4&-1
\end{pmatrix}$
Rappel cours
Produit de deux matrices
Le produit de la matrice $A=(a_{ij})$ de dimensions $n\times p$ par la matrice $B=(b_{ij})$ de dimensions $p\times m$ est la matrice $C=(c_{ij})=A\times B$ de dimensions $n\times m$ telle que $c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+...+a_{ip}b_{pj}=\sum_k=1^p a_{ik}b_{kj}$}
Schématiquement on a:
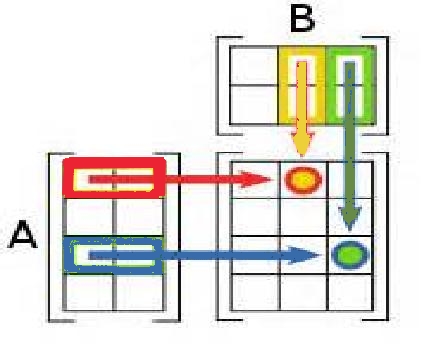
Aide
$A^2=A\times A$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Calculer $A^3$.
Aide
$A^3=A^2\times A$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message