Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Primitive d’une fonction avec exp(u)
Aire sous la courbe et calcul d’intégrale avec exponentielle
Ressources associées et exercices semblables
Aire sous la courbe d’une fonction positive (réf 1218)
exercice
Aire sous une parabole (réf 1214)
exercice
Vidéo de l’exercice
On note $(C_f)$ sa courbe représentative dans le plan muni d'un repère dont les unités sont 3 cm sur l'axe des abscisses et 1 cm sur l'axe des ordonnées.
- Justifier que $f(x) >0$ pour tout réel $x$.
Aide
Rappel: $e^x >0$ pour tout réel $x$.
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Calculer, en unités d'aire puis en cm$^2$, l'aire du domaine limité par $C_f$, l'axe des abscisses, l'axe des ordonnées et la droite d'équation $x=1$.
Rappel cours
Aire et intégrale
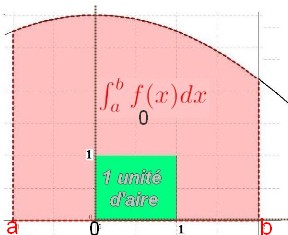
$f$ est une fonction continue et positive sur $[a;b]$ avec $a < b$.
$\int_a^b f(x)dx$ est l'aire, en unités d'aires, du domaine limité par la courbe de $f$, l'axe des abscisses et les droites d'équations $x=a$ et $x=b$.
 Cas de la fonction $e^{u}$
Cas de la fonction $e^{u}$
La fonction $f$ définie sur $I$ par $f(x)=e^{u(x)}$ avec $u$ fonction dérivable sur $I$ est dérivable sur $I$ et $f'(x)=u'(x)e^{u(x)}$Aide
Il faut chercher une primitive de $f$ et notamment de $e^{3x}$
On a $\left(e^{3x}\right)'=3e^{3x}$Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION


 Envoyez votre message
Envoyez votre message