Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Constructions d’intersection dans l’espace avec un tétraèdre
Ressources associées et exercices semblables
Constructions d’intersections dans l’espace-section d’un pavé droit (réf 1301)
exercice
Position de droites et de plans-intersections dans l’espace (réf 1302)
exercice
Fiche méthode représentation paramétrique d’une droite (réf 1295)
méthode
Vidéo de l’exercice
$I$ est un point du segment $[BE]$ et $J$ est un point de $[CE]$ tels que $(IJ)//(BC)$.
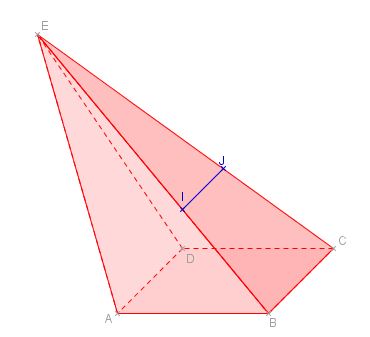
- Montrer que $(IJ)$ est parallèle à $(AD)$.
Rappel cours
Position relative de deux droites
- Les droites $D$ et $\Delta$
Les droites $D$ et $\Delta$ ne sont pas coplanaires
Aucun plan ne contient les deux droites
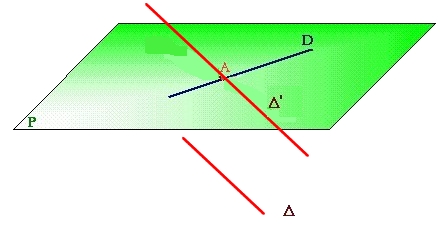
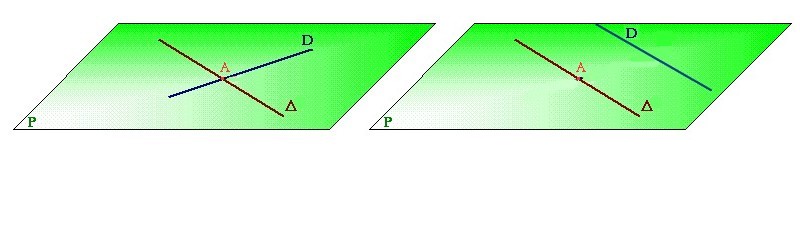
Les droites $D$ et $\Delta$
Les droites $D$ et $\Delta$ ne sont pas coplanaires Les deux droites sont sécantes ou parallèles
Aide
$(IJ)$ est l'intersection des plans $(ABI)$ et $(BCI)$.
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Montrer que $(AI)$ et $(DJ)$ sont sécantes en un point $M$ et construire $M$.
Aide
Les plans $(ABE)$ et $(DCF)$ sont parallèles.
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Déterminer l'intersection $\Delta$ des plans $(ABE)$ et $(CDE)$.
Rappel cours
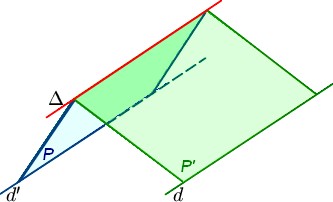
théorème du toit
Lorsque deux plans $P$ et $P'$ sont sécants et contiennent respectivement les droites $d$ et $d'$, l'intersection de $P$ et de $P'$ est une droite $\Delta$ parallèle à $d$ et à $d'$.
Aide
Les droites $(AB)$ et $(CD)$ sont parallèles.
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Montrer que $M$ appartient à $\Delta$.
Aide
Il faut montrer que $M$ est un point commun aux plans $(ABE) et $(CDE)$.
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION