Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Lecture graphique de f'(0)
Identification des coefficients de f
Limites avec exponentielle et utilisation des croissances comparées
Calcul de la dérivée seconde
Étude de la convexité et point d’inflexion
Ressources associées et exercices semblables
Étude d’une fonction à l’aide d’une fonction auxiliaire (réf 1072)
exercice
Vidéo de l’exercice (partie 1)
- Exprimer $f'(x)$ en fonction de $a$ et $b$.
Rappel cours
Cas de la fonction $e^{u}$
La fonction $f$ définie sur $I$ par $f(x)=e^{u(x)}$ avec $u$ fonction dérivable sur $I$ est dérivable sur $I$ et $f'(x)=u'(x)e^{u(x)}$Aide
On pose $u(x)=ax+b$ et $v(x)=e^{-x}$
Solution
Vous devez être abonné pour accéder à ce contenu...
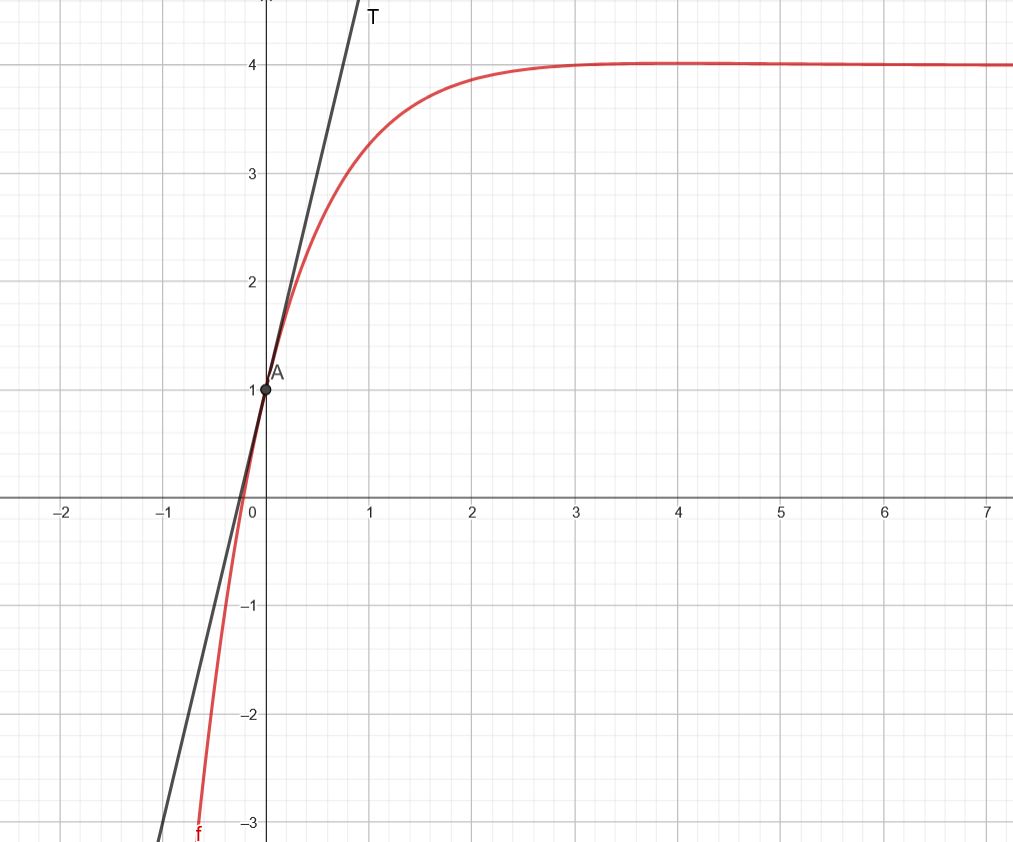
Infos abonnements - En utilisant le graphique, déterminer $f(0)$ et $f'(0)$ et en déduire $a$ et $b$
Rappel cours
Équation de la tangente au point d'abscisse $a$
$f$ est une fonction définie et dérivable en $x=a$.
La tangente à $C_f$ en $a$ a pour coefficient directeur $f'(a)$
et pour équation réduite $ y=f'(a)(x-a)+f(a)$}Aide
Il faut déterminer le coefficient directeur de la tangente au point d'abscisse 0
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer les limites de $f$ en $-\infty$ et $+\infty$ et préciser les asymptotes éventuelles à la courbe.
Rappel cours
limites usuelles
$\displaystyle \lim_{x \rightarrow +\infty}x^n=+\infty$ ($n\in \mathbb{N}^*$)
$\displaystyle \lim_{x \rightarrow +\infty}\dfrac{1}{x^n}=0$ ($n\in \mathbb{N}^*$)
$\displaystyle \lim_{x \rightarrow 0}\dfrac{1}{x^n}=\pm \infty$ ($n\in \mathbb{N}^*$)
Limites de la fonction exponentielle(vue en première)
$\displaystyle \lim_{x \rightarrow -\infty}e^x=0$
$\displaystyle \lim_{x \rightarrow +\infty}e^x=+\infty$ $\displaystyle \lim_{x \rightarrow -\infty}x^n=\pm \infty$ ($n\in \mathbb{N}^*$)
$\displaystyle \lim_{x \rightarrow -\infty}\dfrac{1}{x^n}=0$ ($n\in \mathbb{N}^*$)
$\displaystyle \lim_{x \rightarrow +\infty}\sqrt{x}=+ \infty$ ($n\in \mathbb{N}^*$)
Limites de la fonction $ln$ (chapitre fonction $ln$)
$\displaystyle \lim_{x \rightarrow 0^+}ln(x)=-\infty$
$\displaystyle \lim_{x \rightarrow +\infty}ln(x)=+\infty$
Aide
On peut écrire que $e^{-x}=\dfrac{1}{e^x}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - On rappelle que $f'(x)=(-x-b+1)e^{-x}$ avec $b=-3$ soit $f'(x)=(-x+4)e^{-x}$.
On admet que $f'$ est dérivable.
Calculer $f''(x)$ et étudier la convexité de $f$.
Préciser le ou les points d'inflexion à la courbe $C_f$Rappel cours
Signe de la dérivée seconde
Soit $f$ définie et dérivable sur un intervalle I de $\mathbb{R}$
si $f''(x)>0$ sur $I$ alors $f$ est convexe
si $f''(x)<0$ sur $I$ alors $f$ est concaveSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message