Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Limites de suites
Cas d’indétermination de limites
Limites par comparaison
Ressources associées et exercices semblables
Devoir suites et limites (réf 0968)
devoir
Devoir suites, limites et raisonnement par récurrence (réf 0969)
devoir
- $u_n=2n^2$
Aide
Que devient $2n^2$ quand $n$ devient "infiniment" grand?
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $u_n=\dfrac{1}{n+2}$
Aide
Que devient $n+2$ et donc $\dfrac{1}{n+2}$ quand $n$ devient "infiniment" grand?
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $u_n=-3n^3$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Déterminer les limites ci-dessous si cela est possible.
- $\displaystyle \lim_{n \rightarrow +\infty} u_n+ v_n$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $\displaystyle \lim_{n \rightarrow +\infty} u_n\times v_n$
Rappel cours
Formes indéterminées
Formes indéterminées à retenir $+\infty-\infty~~~~~~0\times \infty$
$\dfrac{0}{0}~~~~\dfrac{\infty}{\infty}$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $\displaystyle \lim_{n \rightarrow +\infty} \dfrac{u_n}{v_n}$
Rappel cours
Limite d'un quotient
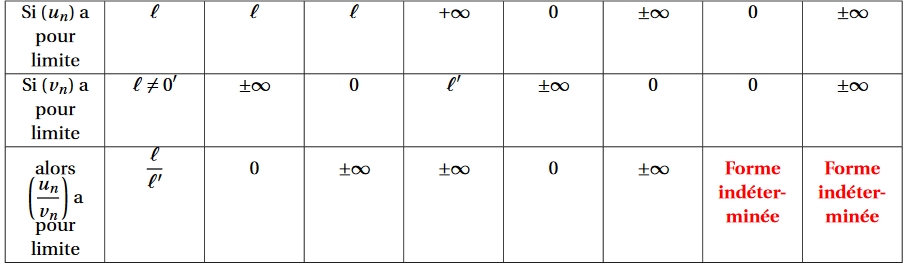
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $\displaystyle \lim_{n \rightarrow +\infty} \dfrac{v_n}{u_n}$
Rappel cours
Limite d'un quotient

Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Calculer $u_0$, $u_1$ et $u_2$.
Montrer que la suite $(u_n)$ n'est ni arithmétique, ni géométrique.Aide
Il faut vérifier que la différence, puis le quotient de deux termes consécutifs n'est pas constant
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Montrer que pour tout $n>0$ on a $u_n=\dfrac{1+\dfrac{2}{n}}{n+\dfrac{1}{n}}$
En déduire la limite de la suite $(u_n)$.Rappel cours
Limite d'un quotient

Aide
On peut factoriser $n$ au numérateur et au dénominateur
Chercher ensuite la limite du numérateur et du dénominateur puis du quotientSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Déterminer $\displaystyle \lim_{n \rightarrow +\infty} \dfrac{1}{n+1}$.
Rappel cours
Limite d'un quotient

Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En utilisant un encadrement de $u_n$, déterminer la limite de $(u_n)$.
Rappel cours
Théorème des gendarmes
Soient trois suites $(u_n)$, $(v_n)$ et $(w_n)$.
Si $\lim_{n\rightarrow+\infty}u_n=\ell$ et $\lim_{n\rightarrow+\infty}w_n=\ell$ et s'il existe un entier $p$ tel que, pour tout $n\geq p$, $u_n\leq v_n\leq w_n$, alors $\lim_{n\rightarrow+\infty}v_n=\ell$.Aide
On a $-1\leq cos(n)\leq 1$
Il faut montrer que $3-\dfrac{1}{n+1}\leq u_n\leq 3+\dfrac{1}{n+1}$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message