Devoir probabilités, variables aléatoires, espérance et loi binomiale (réf 1352) chapitre 8 probabilités, variables aléatoires, loi binomiale et démombrement, séquence 5 exercices de synthèse et devoirs d'entraînement, TERMINALE SPÉCIALITÉ MATHS

Home TERMINALE SPÉCIALITÉ MATHS chapitre 8 probabilités, variables aléatoires, loi binomiale et démombrement séquence 5 exercices de synthèse et devoirs d'entraînement

Devoir probabilités, variables aléatoires, espérance et loi binomiale (réf 1352)

Ressource précédente: Devoir court sur le dénombrement (réf 1351) Ressource suivante: Fiche méthode loi binomiale (réf 1353)

Informations

Vous devez être inscrit pour accéder à ces informations.

Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.

Inscrivez vous gratuitement ici....

Contenu

Probabilités conditionnelles et totales

Loi binomiale: calculs de probabilités et espérance

Loi de probabilités d’une variable aléatoire et espérance

Ressources associées et exercices semblables

| | | |

Exercice 1 (5 points)

Julien doit prendre l'avion; il a prévu de prendre le bus pour se rendre à l'aéroport.
S'il prend le bus de $8$h, il est certain d'être à l'aéroport à temps pour son vol.
Par contre, le bus suivant ne lui permettrait pas d'arriver à temps à l'aéroport.
Julien est parti en retard de son appartement et la probabilité qu'il manque son bus est de $0,8$.
S'il manque son bus, il se rend à l'aéroport en prenant un taxi et il a alors une probabilité de $0,5$ d'être à l'heure à l'aéroport.
On note :
- $B$ l'événement:"Julien réussit à prendre son bus";
- $V$ l'événement: "Julien est à l'heure à l'aéroport pour son vol".

Donner la valeur de $P_B(V)$.

Solution

Vous devez être abonné pour accéder à ce contenu...
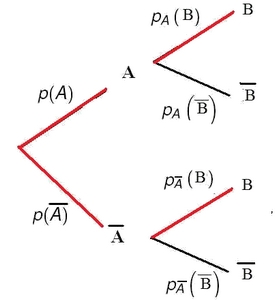
Infos abonnements
Représenter la situation par un arbre pondéré.

Rappel cours

Arbre pondéré
Probabilités sur un arbre pondéré:

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Calculer $p(B\cap V)$ et en donner la signification.

Rappel cours

Probabilité conditionnelle
Soient $A$ et $B$ deux événements avec $p(A)\neq 0$.
La probabilité que l'événement $B$ soit réalisé sachant que l'événement $B$ est réalisé se note $p_A(B)$
et on a $p_A(B)=\dfrac{p(A\cap B)}{p(A)}$.

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Montrer que $P(V) = 0,6$.

Rappel cours

Probabilités totales
Soient $A_1$, $A_2$,...$A_n$ des événements de l'univers $\Omega$ tels que $p(A_1)\neq 0$, $p(A_2)\neq 0$...$p(A_n)\neq 0$ et $B$ un événements.
Si $A_1$, $A_2$,...$A_n$ sont deux à deux disjoints et que leur réunion forme l'univers $\Omega$ alors $A_1$, $A_2$...$A_n$ forment une partition de $\Omega$
et on a $p(B)=p(A_1\cap B)+p(A_2\cap B)+...+p(A_n\cap B)$}
$A$ et $\overline{A}$ forment une partition de l'univers et on a $p(B)=p(A\cap B)+p(\overline{A}\cap B)$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Si Julien est à l'heure à l'aéroport pour son vol, quelle est la probabilité qu'il soit arrivé à l'aéroport en bus ? Justifier.

Rappel cours

Probabilité conditionnelle
Soient $A$ et $B$ deux événements avec $p(A)\neq 0$.
La probabilité que l'événement $B$ soit réalisé sachant que l'événement $B$ est réalisé se note $p_A(B)$
et on a $p_A(B)=\dfrac{p(A\cap B)}{p(A)}$.

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements

Exercice 2 (15 points)

Les compagnies aériennes vendent plus de billets qu'il n'y a de places dans les avions car certains passagers ne se présentent pas à l'embarquement du vol sur lequel ils ont réservé.
On appelle cette pratique le surbooking.
Au vu des statistiques des vols précédents, la compagnie aérienne estime que chaque passager a 5% de chance de ne pas se présenter à l'embarquement.
On considère un vol dans un avion de $200$ places pour lequel $206$ billets ont été vendus.
On suppose que la présence à l'embarquement de chaque passager est indépendante des autres passagers et on appelle $X$ la variable aléatoire qui compte le nombre de passagers se présentant à l'embarquement.

Justifier que $X$ suit une loi binomiale dont on précisera les paramètres.

Rappel cours

Loi binomiale
On considère une répétition de $n$ ($n\in \mathbb{N}^*$) épreuves de Bernoulli indépendantes et on note $p$ la probabilité de succès. %l La variable aléatoire $X$ donnant le nombre de succès obtenus parmi $n$ épreuves de Bernoulli suit une loi binomiale de paramètres $n$ et $p$ notée $\mathbb{B}(n;p)$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
En moyenne, combien de passagers vont-ils se présenter à l'embarquement ?

Rappel cours

Espérance de la loi binomiale
On considère la variable aléatoire $X$ suivant une loi binomiale de paramètres $n$ (nombre d'épreuves de Bernoulli indépendantes répétées) et $p$ (probabilité de l'événement $S$), on a alors: $E(X)=np$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Calculer la probabilité que $201$ passagers se présentent à l'embarquement. Le résultat sera arrondi à $10^{-3}$ près.

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Calculer $P(X \leq 200)$, le résultat sera arrondi à $10^{-3}$ près puis interpréter ce résultat dans le contexte de l'exercice.

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
La compagnie aérienne vend chaque billet à $250$ euros.
Si plus de $200$ passagers se présentent à l'embarquement, la compagnie doit rembourser le billet d'avion et payer une pénalité de $600$ euros à chaque passager lésé.
On note : - $Y$ la variable aléatoire égale au nombre de passagers qui ne peuvent pas embarquer bien qu'ayant acheté un billet; - $C$ la variable aléatoire qui totalise le chiffre d'affaire de la compagnie aérienne sur ce vol.
On admet que $Y$ suit la loi de probabilité donnée par le tableau suivant:
1. Justifier la valeur correspondant à $P(Y = 1)$.
  
  Rappel cours
  
  Probabilités avec la loi binomiale
  $X$ sui la loi binomiale $\mathcal{B}(n;p)$
  $p(X=k)=\begin{pmatrix}n\\p\end{pmatrix}p^k\times (1-p)^{n-k}$
  
  Aide
  
  Il y a un passager refusé si 201 passagers se présentent à l'embarquement
  
  Solution
  
  Vous devez être abonné pour accéder à ce contenu...
  Infos abonnements
2. Compléter la loi de probabilité donnée ci-dessus en calculant $P(Y = 6)$.
  
  Solution
  
  Vous devez être abonné pour accéder à ce contenu...
  Infos abonnements
Justifier que: $C = 51500 - 850Y$.

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Donner la loi de probabilité de la variable aléatoire $C$ sous forme d'un tableau.

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Calculer l'espérance de la variable aléatoire $C$ à l'euro près.
Comparer le chiffre d'affaires obtenu en vendant exactement $200$ billets et le chiffre d'affaires moyen obtenu en pratiquant le surbooking.

Rappel cours

Espérance-variance-écart type
L'espérance de la variable aléatoire $X$ (avec les notations précédentes) est:
$E(X)=x_1p_1+x_2p_2+......+x_np_n=\sum_{i=1}^n p_ix_i$
La variance d'une variable aléatoire $X$ est:
$V(X)=p_1(x_1-E(X))^2+p_2(x_2-E(X))^2+.....+p_n(x_n-E(X))^2=\sum_{i=1}^n p_i(x_i-E(X))^2$
ou bien $V(X)=p_1x_1^2+p_2x_2^2+.....+p_nx_n^2-(E(X))^2=\sum_{i=1}^n p_ix_i^2-(E(X))^2$
L'écart type est égal à la racine carrée de la variance: $\sigma(X)=\sqrt{V(X)}$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements

Vous devez être abonné pour accéder à ce contenu...

Infos abonnements

Ressource précédente: Devoir court sur le dénombrement (réf 1351) Ressource suivante: Fiche méthode loi binomiale (réf 1353)