Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Suite définie par une relation de récurrence
Étude des variations et limite
Suites liées par une relation de récurrence
Algorithme de calcul des termes
Ressources associées et exercices semblables
Devoir suites révisions première (réf 0965)
devoir
Devoir limites de suites (réf 0966)
devoir
Devoir suites et limites (réf 0968)
devoir
Devoir suites, limites et raisonnement par récurrence (réf 0969)
devoir
On admettra que pour tout entier naturel $n$, $u_{n} > 0$.
- On désigne par $f$ la fonction définie sur l'intervalle $]0~;~+\infty[$ par $f(x) = \dfrac{1}{2}\left(x + \dfrac{7}{x}\right)$.
Démontrer que la fonction $f$ admet un minimum.
En déduire que pour tout entier naturel $n$, $u_{n} \geqslant \sqrt{7}$.Rappel cours
Angles associés
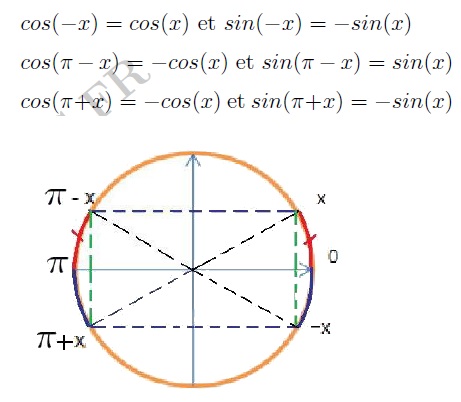
Aide
Il faut dresser le tableau de variation de $f$ en étudiant le signe de $f'(x)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Étudier les variations de la suite $(u_{n})$.
Rappel cours
Étude des variations(différence de deux termes consécutifs)
Pour étudier les variations de $(u_n)$, il faut comparer $u_{n+1}$ et $u_n$.
Exprimer $u_{n+1}-u_n$ en fonction de $n$
Étudier le signe de l'expression obtenue
Si $u_{n+1}-u_n >0 $ alors$u_{n+1} >u_n$ et donc la suite $(u_n)$ est croissante.
Si $u_{n+1}-u_n <0 $ alors$u_{n+1} < u_n$ et donc la suite $(u_n)$ est décroissante.Aide
Il faut étudier le signe de $u_{n+1}-u_n$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - La suite $\left(u_{n}\right)$ est-elle convergente ?
Rappel cours
Suite majorée-suite minorée
Une suite $(u_n)$ est majorée par $M$ si pour tout entier naturel $n$ on a $u_n\leq M$
Une suite $(u_n)$ est minorée par $m$ si pour tout entier naturel $n$ on a $u_n\geq m$
Une suite bornée est une suite à la fois minorée et majorée. Limite d'une suite majorée ou minorée
Si la suite $(u_n)$ est croissante et majorée alors elle est convergente.
Si la suite $(u_n)$ est décroissante et minorée alors elle est convergenteAide
On utilise les questions 2 et 3
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - La limite $\ell$ de cette suite est telle que $\ell =f(\ell)$.
En déduire $\displaystyle \lim_{n \rightarrow +\infty} u_n$.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
$u_0=3$ et $u_{n+1}=\dfrac{u_n+v_n}{2}$ et $v_0=4$ et $v_{n+1}=\dfrac{u_{n+1} + v_n}{2}$.
- Calculer $u_1$, $v_1$, $u_2$ et $v_2$.
Aide
On prendr successivement $n=0$ puis $n=1$ dans les relations données.
Solution
Vous devez être abonné pour accéder à ce contenu...
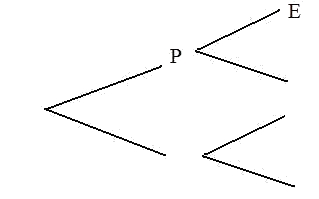
Infos abonnements - On considère l'algorithme ci-dessous.
Compléter cet algorithme pour qu'il affiche les termes des suites $(u_n)$ et $(v_n)$ jusqu'à l'indice 20.
Aide
A chaque passage dans la boucle, on veut calculer les termes $u_{n+1}$ et $v_{n+1}$ en fonction de $U$ et $V$ correspondant aux termes $u_n$ et $v_n$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - L'algorithme ci-dessus affiche les valeurs suivantes(arrondies aux millièmes):
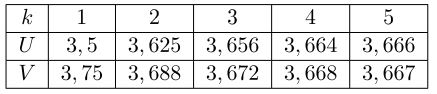
Conjecturer les variations et limites des suite $(u_n)$ et $(v_n)$.Aide
Rappel: conjecturer signifie constater (sans démontrer)
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - . On définit les deux suites $(w_n)$ et $(t_n)$ sur $\mathbb{N}$ par $w_n= v_n- u_n $ et $t_n=\dfrac{u_n + 2v_n}{3}$.
Montrer que $(w_n)$ est géométrique(on précisera sa raison et son premier terme) et que $(t_n)$ est constante.Rappel cours
Suite géométrique
Une suite $(u_n)$ est géométrique s'il existe un réel $q$ tel que pour tout entier naturel $n$, $u_{n+1}=u_n\times q$
$q$ est la raison de la suite.
Le quotient de deux termes consécutifs est égal à la raison soit $\dfrac{u_{n+1}}{u_n}=q$Aide
Il faut montrer que $w_{n+1}=qw_n$ en utilisant $w_{n+1}=v_{n+1}-u_{n+1}$ et les relations définissant les suites $(u_n)$ et $(w_n)$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Exprimer $w_n$ en fonction de $n$ et calculer $t_n$ pour tout entier naturel $n$.
Rappel cours
Forme explicite d'une suite géométrique
Si $(u_n)$ est géométrique de raison $q$ est premier terme $u_0$, on a:
$u_n=u_0\times q^n$
et pour tous entiers $n$ et $p$, $u_n=u_p\times q^{n-p}$Aide
$(w_n)$ est géométrique et $(t_n)$ est constante.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire l'expression de $u_n$ et $v_n$ en fonction de $n$.
Aide
010 On a $w_n=v_n-u_n$ et $t_n=\dfrac{u_n+2v_n}{3}$ soit $3t_n=u_n+2v_n$
On peut donc remplacer $v_n$ par $w_n+u_n$
D'autre part on peut exprimer $w_n$ en fonction de $n$ et on a $t_n=t_0$ (à calculer)Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire la limite des suites $(u_n)$ et $(v_n)$.
Rappel cours
011 Limite de $q^n$ (suite géométrique)
Si $q > 1 $ alors $\displaystyle \lim_{n \rightarrow +\infty}q^n=+\infty$
Si $-1 < q < 1 $ alors $\displaystyle \lim_{n \rightarrow +\infty}q^n=0$Aide
011 $u_n=\dfrac{11}{3}-\dfrac{2}{3\times 4^n}=\dfrac{11}{3}-\dfrac{2}{3}w_n$
Il faut donc chercher la limite de $(w_n)$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message