Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Arbre de probabilités
Probabilités totales
Justifier une loi binomiale
Probabilités avec la loi binomiale
Espérance d’une loi binomiale et interprétation
Ressources associées et exercices semblables
Chaque jour, un athlète doit sauter une haie en fin d'entraînement. Son entraîneur estime, au vu de la saison précédente que
- si l'athlète franchit la haie un jour, alors il la franchira dans $90%$ des cas le jour suivant ;
- si l'athlète ne franchit pas la haie un jour, alors dans $70%$ des cas il ne la franchira pas non plus le lendemain.
On note pour tout entier naturel $n$ :
$R_n$ l'évènement : "L'athlète réussit à franchir la haie lors de la $n$-ième séance"
$p_n$ la probabilité de l'évènement $R_n$. On considère que $p_0 = 0,6$.
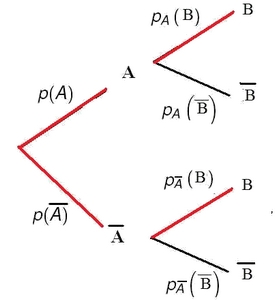
- Soit $n$ un entier naturel, recopier l'arbre pondéré ci-dessous et compléter les
pointillés.
Rappel cours
Arbre pondéré
Probabilités sur un arbre pondéré:
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Justifier en vous aidant de l'arbre que, pour tout entier naturel $n$, on a $p_{n+1} = 0,6p_n + 0,3$
Rappel cours
Probabilités totales
Soient $A_1$, $A_2$,...$A_n$ des événements de l'univers $\Omega$ tels que $p(A_1)\neq 0$, $p(A_2)\neq 0$...$p(A_n)\neq 0$ et $B$ un événements.
Si $A_1$, $A_2$,...$A_n$ sont deux à deux disjoints et que leur réunion forme l'univers $\Omega$ alors $A_1$, $A_2$...$A_n$ forment une partition de $\Omega$
et on a $p(B)=p(A_1\cap B)+p(A_2\cap B)+...+p(A_n\cap B)$}
$A$ et $\overline{A}$ forment une partition de l'univers et on a $p(B)=p(A\cap B)+p(\overline{A}\cap B)$Aide
$p_{n+1}=p(R_{n+1})$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - On considère la suite $\left(u_n\right)$ définie, pour tout entier naturel $n$, par $u_n = p_n - 0,75$.
- Démontrer que la suite $\left(u_n\right)$ est une suite géométrique dont on précisera la raison et le premier terme.
Rappel cours
Suite géométrique
Une suite $(u_n)$ est géométrique s'il existe un réel $q$ tel que pour tout entier naturel $n$, $u_{n+1}=u_n\times q$
$q$ est la raison de la suite.
Le quotient de deux termes consécutifs est égal à la raison soit $\dfrac{u_{n+1}}{u_n}=q$Aide
On a $u_{n+1}=p_{n+1}-0,75=0,6p_n+0,3-0,75$ et on a $p_n=u_n+0,75$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Démontrer que, pour tout entier $n$ naturel $n$ :
$p_n = 0,75 - 0,15 \times 0,6^n$Rappel cours
Forme explicite d'une suite géométrique
Si $(u_n)$ est géométrique de raison $q$ est premier terme $u_0$, on a:
$u_n=u_0\times q^n$
et pour tous entiers $n$ et $p$, $u_n=u_p\times q^{n-p}$Aide
$(u_n)$ suite géométrique et $p_n=u_n+0,75$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire que la suite $\left(p_n\right)$ est convergente et déterminer sa limite $\ell$.
Rappel cours
Limite de $q^n$
$\displaystyle \lim_{n \rightarrow +\infty}q^n=0$ pour $-1< q < 1$
Si $q> 1 $ alors $\displaystyle \lim_{n \rightarrow +\infty}q^n=+\infty$Aide
Chercher la limite de $0,6^n$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Interpréter la valeur de $\ell$ dans le cadre de l'exercice.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Démontrer que la suite $\left(u_n\right)$ est une suite géométrique dont on précisera la raison et le premier terme.
Partie B
Après de nombreuses séances d'entraînement, l'entraineur estime maintenant que l'athlète franchit chaque haie avec une probabilité de $0,75$ et ce indépendamment d'avoir franchi ou non les haies précédentes.
On note $X$ la variable aléatoire qui donne le nombre de haies franchies par l'athlète à l'issue d'un $400$~mètres haies qui comporte $10$~haies,
- Préciser la nature et les paramètres de la loi de probabilité suivie par $X$.
Rappel cours
Loi binomiale
On considère une répétition de $n$ ($n\in \mathbb{N}^*$) épreuves de Bernoulli indépendantes et on note $p$ la probabilité de succès. %l La variable aléatoire $X$ donnant le nombre de succès obtenus parmi $n$ épreuves de Bernoulli suit une loi binomiale de paramètres $n$ et $p$ notée $\mathbb{B}(n;p)$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer, à $10^{-3}$ près, la probabilité que l'athlète franchisse les $10$ haies.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Calculer $p(X \geq 9)$, à $10^{-3}$ près.
Aide
$X\geq 9$ est le contraire de X\leq 8$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Calculer $E(X)$ et en donner l'interprétation.
Rappel cours
Espérance de la loi binomiale
On considère la variable aléatoire $X$ suivant une loi binomiale de paramètres $n$ (nombre d'épreuves de Bernoulli indépendantes répétées) et $p$ (probabilité de l'événement $S$), on a alors: $E(X)=np$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements