Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Vecteur normal à un plan
Équation d’un plan défini par trois points
Représentation paramétrique d’une droite
Recherche du point d’intersection d’une droite et d’un plan
Ressources associées et exercices semblables
Droite orthogonale à un plan dans un cube (réf 1278)
exercice
Équation d’un plan orthogonal à une droite (réf 1279)
exercice
Intersection droite-plan (réf 1282)
exercice
Distance point-plan (réf 1281)
exercice
Vidéo de l’exercice
- Montrer que les points $A$, $B$ et $C$ définissent bien un plan.
Rappel cours
Coordonnées d'un vecteur dans l'espace
L'espace est muni d'un repère quelconque.
Soit $A(x_A;y_A;z_A)$ et $B(x_B;y_B;z_B)$
$\overrightarrow{AB}\begin{pmatrix} x_B-x_A\\ y_B-y_A\\ z_B-z_A \end{pmatrix} $Aide
Il faut vérifier que les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont colinéaires.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Vérifier que le vecteur $\overrightarrow{n}\begin{pmatrix}
2\\
1\\
4
\end{pmatrix}
$ est un vecteur normal au plan $(ABC)$
Rappel cours
Vecteur normal à un plan-équation cartésienne d'un plan
Dans l'espace muni d'un repère othonormé, $P$ est un plan de l'espace, un vecteur $\overrightarrow{n}$ normal à $P$ est un vecteur directeur d'une droite orthogonale à $P$.
Le vecteur $\overrightarrow{n}$ est un vecteur normal au plan $P$ passant par $A$ et $P$ est l'ensemble des points $M(x;y;z)$ vérifiant $\overrightarrow{AM}.\overrightarrow{n}=0$.
$ax+by+cz+d=0$ est une équation cartésienne de $P$ de vecteur normal $\overrightarrow{n}\begin{pmatrix} a\\ b\\ c \end{pmatrix}$Aide
Il faut vérifier que le vecteur normal $\overrightarrow{n}$ est orthogonal aux vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire une équation cartésienne de $(ABC)$.
Rappel cours
Vecteur normal à un plan-équation cartésienne d'un plan
Dans l'espace muni d'un repère othonormé, $P$ est un plan de l'espace, un vecteur $\overrightarrow{n}$ normal à $P$ est un vecteur directeur d'une droite orthogonale à $P$.
Le vecteur $\overrightarrow{n}$ est un vecteur normal au plan $P$ passant par $A$ et $P$ est l'ensemble des points $M(x;y;z)$ vérifiant $\overrightarrow{AM}.\overrightarrow{n}=0$.
$ax+by+cz+d=0$ est une équation cartésienne de $P$ de vecteur normal $\overrightarrow{n}\begin{pmatrix} a\\ b\\ c \end{pmatrix}$Aide
Les coefficients de $x$, $y$ et $z$ dans $ax+by+cz+d=0$ sont donnés par les coordonnées d'un vecteur normal au plan $(ABC)$ et on détermine $d$ en utilisant les coordonnées du point $A$ par exemple
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer une représentation paramétrique de la droite $(DE)$ avec $D(1;3;-2)$ et $E(7;6;10)$.
Aide
La droite a pour vvecteur directeur $\overrightarrow{DE}$ (coefficients du paramètre $t$) et passe par $D$ (ou par $E$).
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Montrer que $(DE)$ est orthogonale au plan $(ABC)$ et déterminer les coordonnées du point d'intersection de $(DE)$ et du plan $P$.
Rappel cours
droite et plan orthogonaux
Une droite $(d)$ est orthogonale à un plan si et seulement si un vecteur directeur de $(d)$ est orthogonal à deux vecteurs directeurs de du plan.
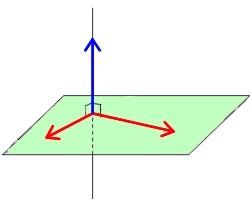
Aide
Il faut vérifier qu'un vecteur directeur de $d$ et un vecteur normal au plan $P$ sont colinéaires.
Il faut écrire une équation d'inconnue $t$ en remplaçant dans l'équation de $P$ les expressions de $x$, $y$ et $z$ données avec la représentation paramétrique de $d$.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message