Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
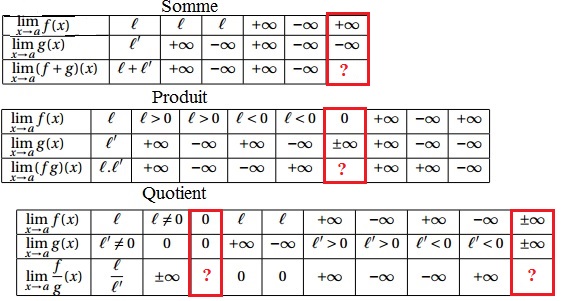
Opérations sur les limites
Limites avec les fonctions « usuelles »
Limites avec exponentielle
Ressources associées et exercices semblables
Limites, cas d’indétermination et asymptotes (réf 1016)
devoir
- $\displaystyle \lim_{x \rightarrow +\infty}f(x)=+\infty$ et
$\displaystyle \lim_{x \rightarrow +\infty}g(x)=3$.
Rappel cours
Opérations sur les limites
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $\displaystyle \lim_{x \rightarrow +\infty}f(x)=-\infty$ et
$\displaystyle \lim_{x \rightarrow +\infty}g(x)=0$ et $g(x)>0$.
Rappel cours
Cas d'indétermination
$+\infty-\infty$
$0\times \pm \infty$
$\dfrac{\pm \infty}{\pm \infty}$
$\dfrac{0}{0}$
Attention, les écritures ci-dessus remplacent les limites mais sont incorrectes...Aide
il y a un cas d'indétermination
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $\displaystyle \lim_{x \rightarrow +\infty}f(x)=2$ et
$\displaystyle \lim_{x \rightarrow +\infty}g(x)=0$ et $g(x)<0$.
Rappel cours
Opérations sur les limites

Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $\displaystyle \lim_{x \rightarrow +\infty}x-\dfrac{1}{x}$ et $\displaystyle \lim_{x \rightarrow 0^+}x-\dfrac{1}{x}$
Aide
Déterminer la limite de chaque terme de la somme
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{3}{5-x}$ et $\displaystyle \lim_{x \rightarrow 5^+}\dfrac{3}{5-x}$
Rappel cours
Opérations sur les limites

Aide
Déterminer la limite de chaque terme du quotient
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Déterminer $\displaystyle \lim_{x \rightarrow -\infty}f(x)$ et interpréter graphiquement ce résultat.
Rappel cours
limite $l$ en $+\infty$ et interprétation graphique
La fonction $f$ est définie sur un intervalle $[a;+\infty[$ et $\ell \in \mathbb{R}$.
$\displaystyle \lim_{x \rightarrow +\infty}f(x)=\ell$ si pour tout intervalle ouvert I contenant $\ell$, il existe $x_0$ tel que pour tout $x>x_0$ on a $f(x)\in $ I
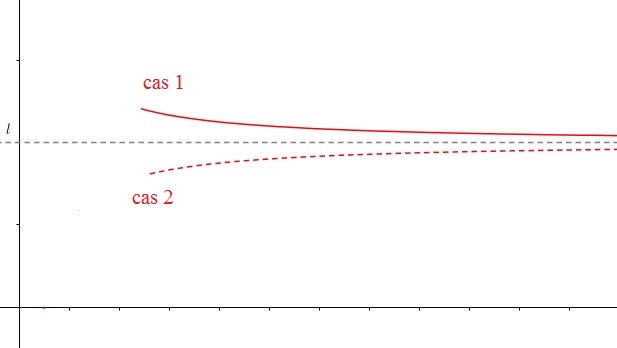
La droite d'équation $y=\ell$ est asymptote à la courbe en $+\infty$Aide
Rappel: $\displaystyle \lim_{x \rightarrow -\infty}e^x=0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Montrer que pour tout réel $x\neq 0$ on a $f(x)=e^x\left(\dfrac{e^x}{x}-3\right)$ et en déduire $\displaystyle \lim_{x \rightarrow +\infty}f(x)=0$
Rappel cours
Cas d'indétermination
$+\infty-\infty$
$0\times \pm \infty$
$\dfrac{\pm \infty}{\pm \infty}$
$\dfrac{0}{0}$
Attention, les écritures ci-dessus remplacent les limites mais sont incorrectes... Croissances comparées de $x^n$ et $e^x$
$n\in \mathbb{N}^*$
$\displaystyle \lim_{x \rightarrow +\infty}\dfrac{e^x}{x}=+\infty$
et $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{e^x}{x^n}=+\infty$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message