Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Vecteurs de l’espace dans un cube
Vecteurs égaux
Ressources associées et exercices semblables
Somme de vecteurs de l’espace dans un cube (réf 1236)
exercice
Vecteurs colinéaires et alignement dans l’espace (réf 1237)
exercice
Vecteurs colinéaires et alignement dans l’espace (réf 1238)
exercice
Caractérisation d’une droite de l’espace (réf 1239)
exercice
Vidéo de l’exercice
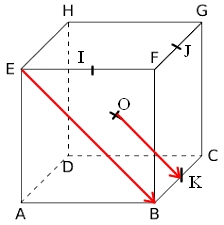
$I$, $J$ et $K$ sont les milieux respectifs des côtés $[EF]$, $FG]$ et $[BC]$ et $O$ est le centre du cube.
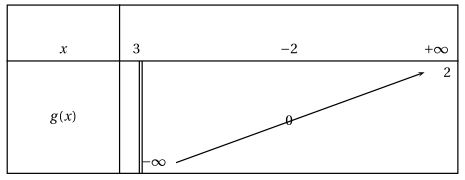
- Donner (sans justifier) un vecteur égal à chacun des vecteurs suivant.
$\overrightarrow{DC}~~~~~~~~~\overrightarrow{JK}~~~~~~~~\overrightarrow{EJ}~~~~~~~~\overrightarrow{OB}$Rappel cours
vecteurs égaux
Si $A$, $B$, $C$ et $D$ sont quatre points distincts, les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{CD}$ sont égaux si et seulement si $ABDC$ est un parallélogramme.
$D$ est l'image de $C$ par la translation de vecteur $\overrightarrow{AB}$.Solution
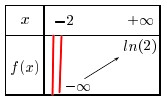
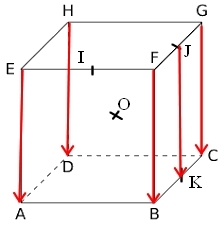
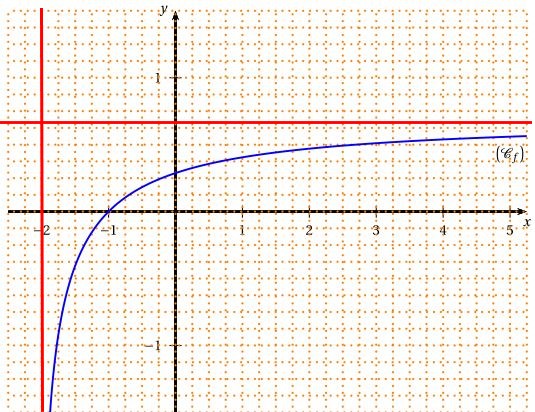
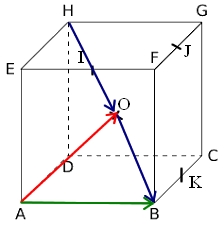
- Compléter
$\overrightarrow{HE}+\overrightarrow{AK}=\overrightarrow{......}$
$\overrightarrow{EB}=2\overrightarrow{.....}$
$\overrightarrow{AO}+\overrightarrow{HO}=\overrightarrow{....}$Rappel cours
relation de Chasles
$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$Aide
on peut utiliser les vecteurs égaux dans le cube pour calculer les sommes
Solution


 Envoyez votre message
Envoyez votre message