Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Algorithme de calcul des termes d’une suite
Suites liées par une relation de récurrence
Étude des variations
Étude de la convergence (suite croissante majorée)
Ressources associées et exercices semblables
Suites liées par une relation de récurrence (ex BAC) (réf 0957)
exercice
Vidéo de l’exercice
- On considère l'algorithme suivant :
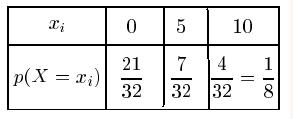
Reproduire et compléter le tableau suivant, en faisant fonctionner cet algorithme pour $a = 4$, $b = 9$ et $N = 2$. Les valeurs successives de $u$ et $v$ seront arrondies au millième.

Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements -
- Démontrer par récurrence que, pour tout entier naturel $n$, on a : $u_{n} > 0$
puis que $v_{n} > 0$.Rappel cours
Raisonnement par récurrence
On note $P_n$ une propriété définie pour tout entier naturel $n$.
Initialisation:
$P_0$ est vraie
Hérédité:
Si $P_n$ est vraie alors$P_{n+1}$ est vraie.
on a alors $P_n$ vraie pour tout entier naturel $n$.Aide
On peut poser $P_n$ la propriété $u_n >0$
Ne pas oublier de vérifier que $P_0$ est vraie
On veut finalement montrer que $\dfrac{u_{n}+ v_{n}}{2}$ est strictement positif sachant que $u_n$ et $v_n$ sont strictement positifs.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Démontrer que, pour tout entier naturel $n$ : $v^2_{n+1} - u^2_{n+1} = \left(\dfrac{u_{n} - v_{n}}{2}\right)^2$.
En déduire que, pour tout entier naturel $n$, on a $u_{n} \leq v_{n}$.Aide
en développant (u_n+v_n)^2$
On a $v^2_{n+1} - u^2_{n+1}=(u_{n+1}+v_{n+1})(u_{n+1}-v_{n+1})$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Démontrer par récurrence que, pour tout entier naturel $n$, on a : $u_{n} > 0$
-
- Démontrer que la suite $\left(u_{n}\right)$ est croissante.
Aide
On peut étudier le signe de $u_{n+1}-u_n$ en utilisant $u_{n+1}=\dfrac{u_n+v_n}{2}$ et le résultat précédent.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Comparer $v^2_{n+1}$ et $v^2_{n}$. En déduire le sens de variation de la suite $\left(v_{n}\right)$.
Aide
Si on compare les carrés $v_{n+1}^2$ et $v_n^2$ on peut comparer aussi $v_{n+1}$ et $v_n$ puisque $v_n>0$ pour tout entier naturel $n$ et la fonction carré est strictement croissante sur $[;+\infty[$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Démontrer que la suite $\left(u_{n}\right)$ est croissante.
- Démontrer que les suites $\left(u_{n}\right)$ et $\left(v_{n}\right)$ sont convergentes.
Rappel cours
Limite d'une suite majorée ou minorée
Si la suite $(u_n)$ est croissante et majorée alors elle est convergente.
Si la suite $(u_n)$ est décroissante et minorée alors elle est convergenteAide
Il faut utiliser les variations des suites $(u_n)$ et $(v_n)$ et trouver un majorant pour la suite $(u_n)$ et un minorant pour la suite $(v_n)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Dans la suite, $a$ et $b$ sont deux réels tels que $0 < a < b$.
On considère les suites $\left(u_{n}\right)$ et $\left(v_{n}\right)$ définies par :
$u_{0} = a$, $v_{0} = b$ et, pour tout entier naturel $n$ :
$u_{n+1} = \dfrac{u_{n}+ v_{n}}{2}$ et $v_{n+1} = \sqrt{\dfrac{u_{n}^2 + v_{n}^2}{2}}$


 Envoyez votre message
Envoyez votre message