Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Justifier que trois points définissent un plan
Justifier qu’un vecteur est normal à un plan
Déterminer une équation d’un plan
Ressources associées et exercices semblables
Intersection d’un plan avec une droite (réf 1276)
exercice
Position relative d’une droite et d’un plan (réf 1277)
exercice
Droite orthogonale à un plan dans un cube (réf 1278)
exercice
- Montrer que les points $A$, $B$ et $C$ définissent bien un plan.
Rappel cours
Coordonnées d'un vecteur dans l'espace
L'espace est muni d'un repère quelconque.
Soit $A(x_A;y_A;z_A)$ et $B(x_B;y_B;z_B)$
$\overrightarrow{AB}\begin{pmatrix} x_B-x_A\\ y_B-y_A\\ z_B-z_A \end{pmatrix} $
caractérisation vectorielle d'un plan
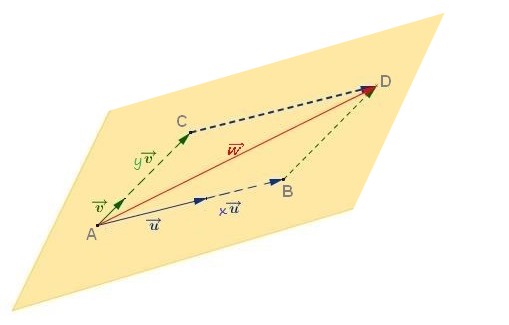
Soit $A$ et les vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ non colinéaires de l'espace, l'ensemble des points $M$ tels que $\overrightarrow{AM}=x\overrightarrow{u}+y\overrightarrow{v}$ avec $x$ et $y$ réels est le plan $(ABC)$ avec $\overrightarrow{AB}=\overrightarrow{u}$ et $\overrightarrow{AC}=\overrightarrow{v}$.
$\overrightarrow{u}$ et $\overrightarrow{v}$ sont des vecteurs directeurs du plan $(ABC)$
Aide
Il faut vérifier que les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ ne sont pas colinéaires.
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Vérifier que le vecteur $\overrightarrow{n}\begin{pmatrix}
1\\
2\\
-2
\end{pmatrix}
$ est un vecteur normal au plan $(ABC)$
Rappel cours
Vecteur normal à un plan-équation cartésienne d'un plan
Dans l'espace muni d'un repère othonormé, $P$ est un plan de l'espace, un vecteur $\overrightarrow{n}$ normal à $P$ est un vecteur directeur d'une droite orthogonale à $P$.
Le vecteur $\overrightarrow{n}$ est un vecteur normal au plan $P$ passant par $A$ et $P$ est l'ensemble des points $M(x;y;z)$ vérifiant $\overrightarrow{AM}.\overrightarrow{n}=0$.
$ax+by+cz+d=0$ est une équation cartésienne de $P$ de vecteur normal $\overrightarrow{n}\begin{pmatrix} a\\ b\\ c \end{pmatrix}$Aide
Il faut vérifier que le vecteur normal $\overrightarrow{n}$ est orthogonal aux vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - En déduire une équation cartésienne de $(ABC)$.
Rappel cours
Vecteur normal à un plan-équation cartésienne d'un plan
Dans l'espace muni d'un repère othonormé, $P$ est un plan de l'espace, un vecteur $\overrightarrow{n}$ normal à $P$ est un vecteur directeur d'une droite orthogonale à $P$.
Le vecteur $\overrightarrow{n}$ est un vecteur normal au plan $P$ passant par $A$ et $P$ est l'ensemble des points $M(x;y;z)$ vérifiant $\overrightarrow{AM}.\overrightarrow{n}=0$.
$ax+by+cz+d=0$ est une équation cartésienne de $P$ de vecteur normal $\overrightarrow{n}\begin{pmatrix} a\\ b\\ c \end{pmatrix}$Aide
Les coefficients de $x$, $y$ et $z$ dans $ax+by+cz+d=0$ sont donnés par les coordonnées d'un vecteur normal au plan $(ABC)$ et on détermine $d$ en utilisant les coordonnées du point $A$ par exemple
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION