Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Équations trigonométriques
Étude d’une fonction avec sinus
Fonction périodique
Ressources associées et exercices semblables
Devoir trigonométrie mesure principale et équations (réf 0748)
devoir
Devoir trigonométrie (réf 0750)
devoir
Fiche méthode résolution d’équations trigonométriques (réf 0754)
méthode
$-\dfrac{4\pi}{3}~~;~~~~~~~-\dfrac{13\pi}{2}~~;~~~~~~~-\dfrac{5\pi}{6}~~;~~~~~~~-\dfrac{21\pi}{4}~~;~~~~~~~\dfrac{29\pi}{6}~~;~~~~~~~317 \pi$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Compléter
- $ cos (-\dfrac{4\pi}{3})=cos(.....)=...$
- $ sin (-\dfrac{13\pi}{2})=sin(...)=...$
- $ cos (-\dfrac{5\pi}{6})=-cos(....)=...$
- $ cos (-\dfrac{21\pi}{4})=cos(...)=...$
- $ sin (\dfrac{29\pi}{6})=sin (...)=...$
- $ sin (317 \pi)=sin(...)=...$
Rappel cours
Valeurs remarquables du cos et du sin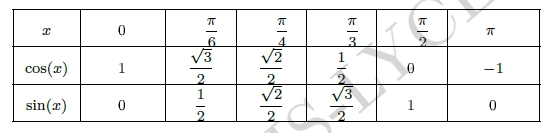
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- $\sin x = -\dfrac{\sqrt{2}}{2}$ avec $x \in [0;2\pi[$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $\cos x = -\dfrac{\sqrt{3}}{2}$ avec $x \in ]-\pi;\pi]$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $\sin x \leq \dfrac{1}{2}$ avec $x \in ]-\pi;\pi]$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $2\cos x - \sqrt{3}>0$ avec $x \in [0;2\pi[$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Rappel cours
$cos^2(x)+sin^2(x)=1$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Montrer que $f$ est impaire.
Rappel cours
$f$ définie sur $D$ est impaire si pour tout réel $x\in D$ on a $-x\in D$ et $f(-x)=f(x)$.
Aide
On peut utiliser $sin(x)=-sin(x)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - On rappelle que la dérivée de $sin(x)$ est $cos(x)$.
Calculer $f'(x)$ et étudier son signe et en déduire les variations de $f$.Aide
Rappel $-1\leq cos(x)\leq 1$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer les abscisses des points de la courbe pour lesquels la tangente à la courbe $C_f$ est parallèle à l'axe des abscisses.
Rappel cours
Le coefficient directeur de la tangente à la courbe de $f$ au point d'abscisses $x$ est $f'(x)$
Aide
Une droite est parallèle à l'axe des abscisses a pour coefficient directeur est $0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Montrer que la courbe est entre deux droites dont on donnera les équations réduites.
Aide
On a $-1\leq sin(x)\leq 1$ donc on peut encadrer $f(x)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Tracer les deux droites de la question précédente puis compléter le tracé de la courbe ci-dessous.
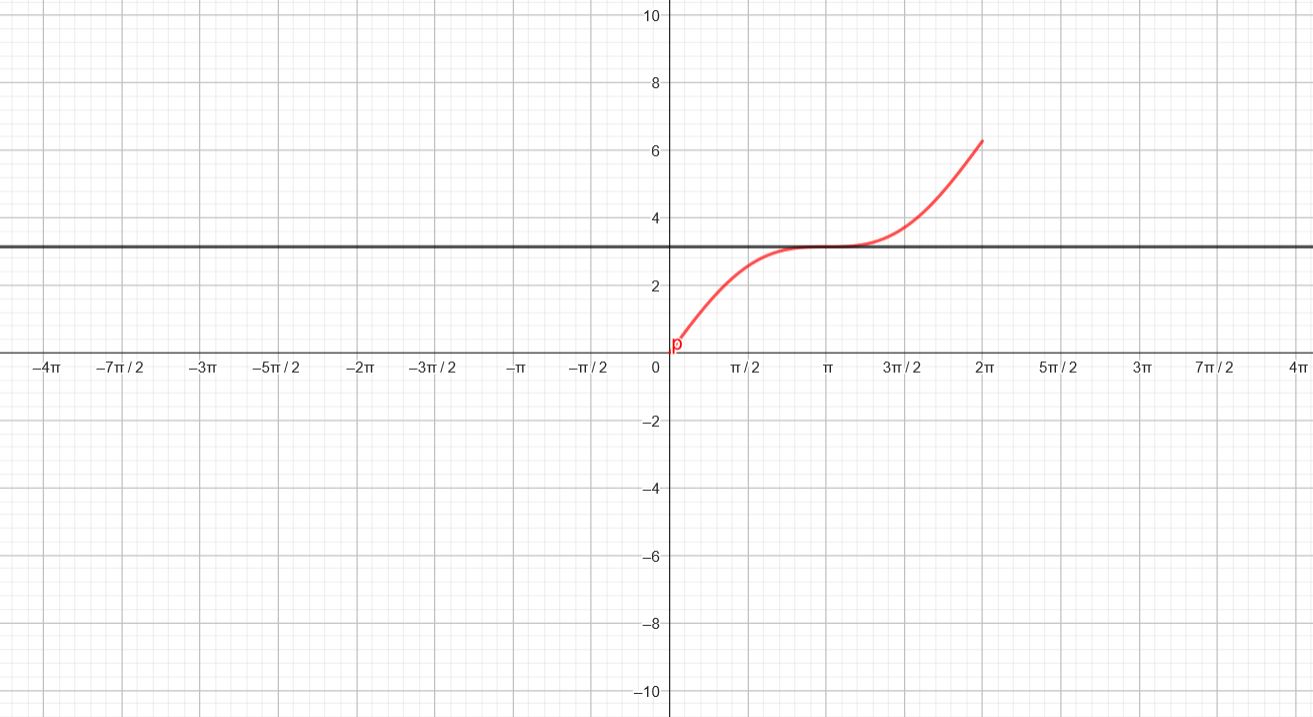
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message