Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Arbre de probabilités
Probabilités conditionnelles
Probabilités totales
Ressources associées et exercices semblables
Probabilités conditionnelles et totales (réf 0868)
exercice
Calcul d’une probabilité conditionnelle (réf 0870)
exercice
Calculs de probabilités avec un arbre (d’après BAC) (réf 0873)
exercice
- $D$ l'évènement « la pièce présente un défaut »
- $A$ l'évènement « la pièce est acceptée au contrôle »
- $E$ l'évènement « le contrôle est défectueux » (la pièce a un défaut et est acceptée à l'issue du contrôle).
On note $p$ la probabilité qu'une pièce prise au hasard parmi les pièce fabriquées ne présente pas de défaut.
La probabilité qu'une pièce n'ayant pas de défaut soit refusée est de 0,01.
La probabilité qu'une pièce ayant un défaut soit acceptée est de 0,05.
\medskip Partie 1
- Construire un arbre pondéré illustrant la situation.
Rappel cours
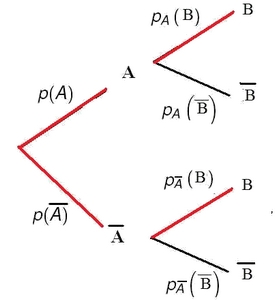
Arbre pondéré
Probabilités sur un arbre pondéré:
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Calculer en fonction de $p$ la probabilité de $E$.
Rappel cours
Probabilité conditionnelle
Soient $A$ et $B$ deux événements avec $p(A)\neq 0$.
La probabilité que l'événement $B$ soit réalisé sachant que l'événement $B$ est réalisé se note $p_A(B)$
et on a $p_A(B)=\dfrac{p(A\cap B)}{p(A)}$.Aide
$E$ est l'événement la pièce a un défaut et est acceptée donc se note $D\cap A$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Calculer, en fonction de p, la probabilité la pièce soit acceptée.
Rappel cours
Probabilités totales
Soient $A_1$, $A_2$,...$A_n$ des événements de l'univers $\Omega$ tels que $p(A_1)\neq 0$, $p(A_2)\neq 0$...$p(A_n)\neq 0$ et $B$ un événements.
Si $A_1$, $A_2$,...$A_n$ sont deux à deux disjoints et que leur réunion forme l'univers $\Omega$ alors $A_1$, $A_2$...$A_n$ forment une partition de $\Omega$
et on a $p(B)=p(A_1\cap B)+p(A_2\cap B)+...+p(A_n\cap B)$}
$A$ et $\overline{A}$ forment une partition de l'univers et on a $p(B)=p(A\cap B)+p(\overline{A}\cap B)$Aide
On veut calculer $p(A)$ et il faut utiliser la formule des probabilités totales.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - On s'intéresse à la probabilité qu'une pièce acceptée soit réellement sans défaut (c'est à dire la probabilité
que la pièce soit sans défaut sachant qu'elle a été acceptée au contrôle).
Montrer que cette probabilité, notée $f(p)$, est définie par $f(p) =\dfrac{99p}{94p + 5}$.Aide
La probabilité que la pièce soit sans défaut sachant qu'elle a été acceptée au contrôle se note $p_A(\overline{D})$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer alors la valeur minimale, arrondie aux centièmes, de p pour que plus de 99% des pièces
acceptées n'aient pas de défaut.
Aide
On veut $f(p)> 0,99$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message