Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Probabilités avec un tableau à double entrée
Probabilités avec un arbre
Probabilités conditionnelles et totales
Loi de probabilités et espérance
Ressources associées et exercices semblables
Devoir probabilités et variables aléatoires (réf 0898)
devoir
Devoir probabilités, arbre, loi de probabilité et espérance (réf 0899)
devoir
Fiche méthodes calculs de probabilités (réf 902)
méthode
Aie mémoire probabilités et variables aléatoires (réf 0903)
mémo
Dans le cas d'un conseiller financier mal informé, le cours ne monte pas dans 60% des cas. On considère que 20% des conseillers financiers sont bien informés. Un client choisit au hasard un conseiller financier qui lui recommande une valeur.
On note :
- $I$ est l'événement : "le conseiller est bien informé"
- $C$ est l'événement : "le cours monte "
- Compléter le tableau suivant:

Aide
Compléter d'abord la dernière colonne du tableau avec la donnée "20% des conseillers financiers sont bien informés"
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer la probabilité de l'événement: "Le conseiller est bien informé et le cours monte".
Aide
L'événement: " Le conseiller est bien informé et le cours monte" se note $C\cap I$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Que signifie $I \cap \overline{C}$?
Calculer $p(I \cap \overline{C})$.Aide
On veut que le conseiller soit bien informé et que le cours ne monte pas
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Sachant que le cours de la valeur est monté, quelle est la probabilité que le conseiller choisi soit mal informé.
Aide
Il faut déterminer le nombre de conseillers mal informés parmi les 46 cas où le cours est monté.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Que signifie $ C \cup I$?
Calculer la probabilité de cet événement.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
-la puissance du véhicule : il a le choix entre deux catégories A ou B ;
- l'équipement : voiture climatisée ou non climatisée.
Une étude statistique portant sur un grand nombre de clients a permis d'établir que 60% des clients louent une voiture de catégorie A et que, parmi eux, 20% désirent la climatisation. En revanche, 60% des clients préférant la catégorie B optent pour la climatisation.
On note les événements:
-A:"le véhicule loué est de catégorie A"
- C: " le véhicule loué est équipé de la climatisation"
Partie 1 (6 points)
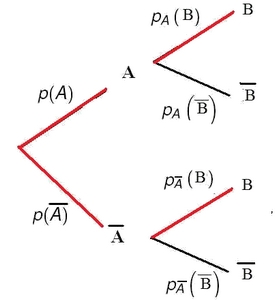
- Traduire à laide d'un arbre pondéré la situation décrite ci-dessus.
Rappel cours
Arbre pondéré
Probabilités sur un arbre pondéré:
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Dans cette question, on donnera des résultats numériques exacts. On choisit au hasard un client et on définit les événements suivants :
"Le client a choisi une voiture de catégorie A climatisée" et "Le client a choisi une voiture climatisée".
Déterminer la probabilité de ces événements.Rappel cours
Probabilité de l'événement $A\cap B$
Soient $A$ et $B$ deux événements avec $p(A)\neq 0$, on a
$p(A\cap B)=p(A)\times p_A(B)$
Probabilités totales
Soient $A_1$, $A_2$,...$A_n$ des événements de l'univers $\Omega$ tels que $p(A_1)\neq 0$, $p(A_2)\neq 0$...$p(A_n)\neq 0$ et $B$ un événements.
Si $A_1$, $A_2$,...$A_n$ sont deux à deux disjoints et que leur réunion forme l'univers $\Omega$ alors $A_1$, $A_2$...$A_n$ forment une partition de $\Omega$
et on a $p(B)=p(A_1\cap B)+p(A_2\cap B)+...+p(A_n\cap B)$}
$A$ et $\overline{A}$ forment une partition de l'univers et on a $p(B)=p(A\cap B)+p(\overline{A}\cap B)$Aide
Utiliser la formule des probabilités totales pour calculer $p(C)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Quelle est la probabilité pour que la voiture choisie soit de catégorie A, sachant qu'elle est climatisée ?
Rappel cours
Probabilité conditionnelle
Soient $A$ et $B$ deux événements avec $p(A)\neq 0$.
La probabilité que l'événement $B$ soit réalisé sachant que l'événement $B$ est réalisé se note $p_A(B)$
et on a $p_A(B)=\dfrac{p(A\cap B)}{p(A)}$.Aide
Utiliser $p(A\cap C)=p(C)\times p_C(A)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Partie 2
Le coût d'une journée de location d'une voiture de catégorie A est de 80 euros par jour et pour la catégorie B de 110 euros par jour.
Pour chacune de ces deux catégories, le supplément pour la climatisation est de 15 euros.
- Compléter le tableau ci-dessous correspondant aux différents coût possibles pour une journée de location en justifiant les valeurs obtenues pour les probabilités:

Rappel cours
Variable aléatoire et loi de probabilité
Une variable aléatoire discrète est une fonction définie de $\Omega$ dans $\mathbb{R}$ qui a tout élément $x_i$ de $\Omega$ associe un nombre réel.
Définir la loi de probabilité d'une variable aléatoire prenant les valeurs $\left\lbrace x_1;x_2;x_3;......x_n\right\rbrace $, c'est déterminer la probabilité d'obtenir la valeur $X=x_i$ pour tout élément de $\left\lbrace x_1;x_2;x_3;......x_n\right\rbrace $Aide
Il faut identifier les quatre cas possibles sur l'arbre et associer le coût correspondant ainsi que la probabilité d'obtenir ce coût.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Le loueur affirme dans sa publicité: "Chez ALIZE, la journée de location revient en moyenne à moins de 100 euros".
Est-ce justifié compte tenu des données disponibles?Rappel cours
Espérance-variance-écart type
L'espérance de la variable aléatoire $X$ (avec les notations précédentes) est:
$E(X)=x_1p_1+x_2p_2+......+x_np_n=\sum_{i=1}^n p_ix_i$
La variance d'une variable aléatoire $X$ est:
$V(X)=p_1(x_1-E(X))^2+p_2(x_2-E(X))^2+.....+p_n(x_n-E(X))^2=\sum_{i=1}^n p_i(x_i-E(X))^2$
ou bien $V(X)=p_1x_1^2+p_2x_2^2+.....+p_nx_n^2-(E(X))^2=\sum_{i=1}^n p_ix_i^2-(E(X))^2$
L'écart type est égal à la racine carrée de la variance: $\sigma(X)=\sqrt{V(X)}$Aide
Il faut calculer l'espérance avec les données du tableau précédent.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message