Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Déterminer une image avec la courbe de la fonction
Ressources associées et exercices semblables
lecture graphique des antécédents (réf 0191)
exercice
lectures graphiques (réf 0192)
exercice
Vidéo de l’exercice
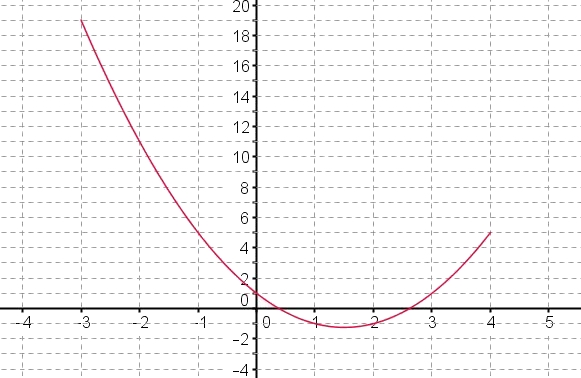
- Déterminer l'image de 1 par $f$
Rappel cours
Ensemble de définition
L'ensemble de définition d'une fonction $f$ est l'ensemble des valeurs pour lesquelles on peut calculer l'image par $f$.
Par exemple, l'ensemble de définition de la fonction $f$ définie par $f(x)=\dfrac{1}{x+2}$ est $\mathbb{R}\setminus \lbrace -2\rbrace$ car le dénominateur doit être différent de $0$.Aide
Il faut déterminer l'ordonnée du point de la courbe d'abscisse 1.
Solution
Sur le graphique, on a:
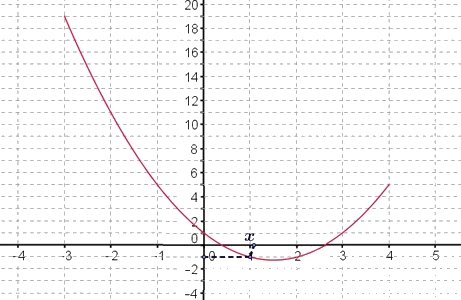
Le point de la courbe d'abscisse 1 a pour ordonnée $-1$.
Remarque
On peut noter $f(1)=-1$. - Déterminer $f(-1)$
Aide
Il faut déterminer l'ordonnée du point de la courbe d'abscisse $-1$.
Solution
Sur le graphique, on a:
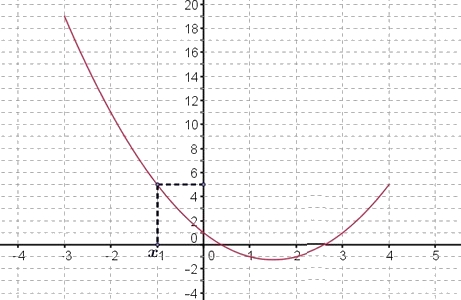
Le point de la courbe d'abscisse $-1$ a pour ordonnée 5.
Remarque
$f(-1)=5$ se lit "l'image de $-1$ par $f$ est 5. - Peut-on déterminer l'image de 5 par $f$?
Aide
La question est 5 appartient-il à l'ensemble de définition de $f$?
Solution
Il n'y a pas de point de la courbe d'abscisse 5
Remarque
L'ensemble de définition de $f$ est $[-3;4]$ et $5\notin [-3;4]$.


 Envoyez votre message
Envoyez votre message