Envoyez votre messageInformations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Aire d’un triangle
Expression de l’aire en fonction de x
Recherche du maximum d’une fonction
Ressources associées et exercices semblables
coûts-recettes et bénéfices (réf 0223)
exercice
volume maximal d’un boîte (réf 0225)
exercice
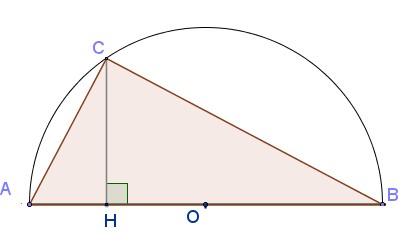
On note $AH=x$
- Exprimer $CH$ en fonction de $x$.
On distinguera les cas $x\leq 5 $ ET $x>5$
Aide
On peut utiliser le triangle $OCH$ rectangle en $H$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - On note $A$ la fonction qui à $x$ associe l'aire du triangle $ABC$.
Quel est l'ensemble de définition de la fonction $A$?
Exprimer $A(x)$ en fonction de $x$.Aide
Le point $H\in [AB]$.
Rappel: l'aire d'un triangle est $A=\dfrac{\text{base}\times \text{hauteur}}{2}$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En utilisant la calculatrice, conjecturer(émettre une hypothèse sans la prouver) la position de $C$ pour laquelle l'aire du triangle est maximale.
Aide
On peut utiliser le MENU TABLE de la calculatrice.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - On donne ci-dessous la représentation graphique de la fonction $A$.
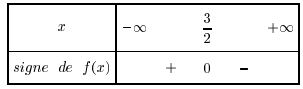
Vérifier que la conjecture émise à la question précédente est cohérente avec le graphique.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer le nombre de positions du point $C$ pour lesquelles l'aire du triangle est de 15 cm$^2$.
Contrôler les solutions obtenues par le calcul.Aide
On cherche le nombre de points de la courbe ayant une ordonnée égale à 15.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire graphiquement les positions possibles du point $C$ pour lesquelles l'aire du triangle est inférieure ou égale à 15 cm$^2$.
Aide
Il faut déterminer les abscisses des points de la courbe dont l'ordonnée est inférieure ou égale à 15.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements