Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Déterminer la convexité connaissant la courbe de la dérivée
Point d’inflexion
Ressources associées et exercices semblables
Lecture graphique de la convexité (réf 1059)
exercice
Déterminer la convexité connaissant la dérivée (réf 1060)
exercice
Identifier la courbe de la dérivée et de la dérivée seconde (réf 1067)
exercice
Vidéo de l’exercice

- Déterminer la convexité de $f$.
Rappel cours
Convexité et variations de la dérivée
Soit $f$ une fonction dérivable sur un intervalle I et $\mathcal{C}_f$ sa courbe représentative.
$f$ est convexe sur I si la courbe $\mathcal{C}_f$ est au-dessus de ses tangentes.
Dans le cas contraire($\mathcal{C}_f$ en-dessous de ses tangentes), $f$ est concave.Aide
Il faut dresser le tableu de variation de $f'$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - La courbe admet-elle un point d'inflexion? Si oui pour quelle valeur de $x$?
Rappel cours
point d'inflexion et dérivée seconde
si $f"(x)$ s'annule et change de signe en $x=x_A$ alors la courbe admet un point d'inflexion au point $A$.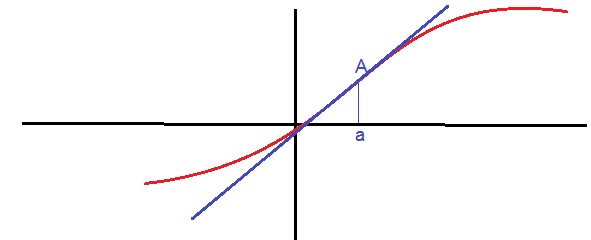
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION


 Envoyez votre message
Envoyez votre message