Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Identifier une fonction convexe ou concave
Déterminer graphiquement un point d’inflexion
Ressources associées et exercices semblables
Convexité et dérivée seconde (réf 1061)
exercice
Étude de la convexité d’un polynôme de degré 2 (réf 1062)
exercice
Étude de la convexité d’un polynôme de degré 3 (réf 1063)
exercice
Fiche méthode théorème des valeurs intermédiaires (réf 1077)
méthode
- fig1
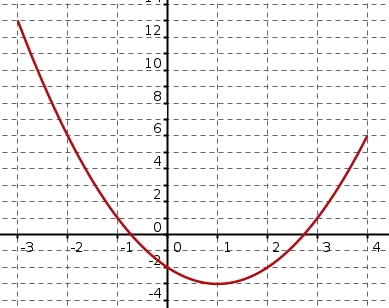
Rappel cours
Convexité et tangentes
Soit $f$ une fonction dérivable sur un intervalle I et $\mathcal{C}_f$ sa courbe représentative.
$f$ est convexe sur I si la courbe $\mathcal{C}_f$ est au-dessus de ses tangentes.
Dans le cas contraire, $\mathcal{C}_f$ en-dessous de ses tangentes), $f$ est concave.Aide
On peut éventuellement tracer à main levée quelques tangentes à la courbe
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Fig 2
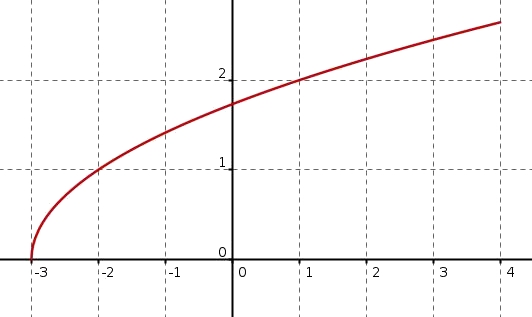
Aide
On peut éventuellement tracer à main levée quelques tangentes à la courbe
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - fig 3
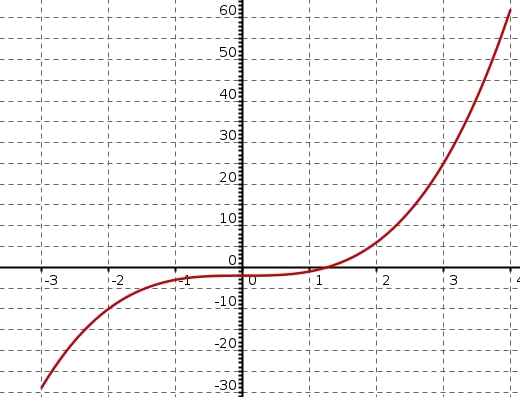
Aide
On peut éventuellement tracer à main levée quelques tangentes à la courbe, notamment la tangente au point d'abscisse 1
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION


 Envoyez votre message
Envoyez votre message