Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Limite d’une fonction rationnelle en l’infini
Cas d’indétermination oo/oo
Ressources associées et exercices semblables
Limite d’un polynôme en l’infini (réf 0991)
exercice
Limite d’une fonction rationnelle en l’infini (réf 0992)
exercice
Limite d’une fonction rationnelle en un point (réf 0993)
exercice
Limites d’une fonction rationnelle en un point (réf 0995)
exercice
- $f(x)=\dfrac{x^2-2}{x-2}$ définie sur $\mathbb{R}\setminus\lbrace 2 \rbrace$.
Rappel cours
Cas d'indétermination
$+\infty-\infty$
$0\times \pm \infty$
$\dfrac{\pm \infty}{\pm \infty}$
$\dfrac{0}{0}$
Attention, les écritures ci-dessus remplacent les limites mais sont incorrectes...Aide
En $-\infty$ et $+\infty$, il y a un cas d'indétermination donc il faut factoriser par le terme de plus haut degré au numérateur et au dénominateur soit $x^2$ au numérateur et $x$ au dénominateur.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $f(x)=\dfrac{x^2-2}{x^3+3x+6}$ définie sur $\mathbb{R}$ et interpréter graphiquement le résultat obtenu (asymptote).
Rappel cours
limite $l$ en $+\infty$ et interprétation graphique
La fonction $f$ est définie sur un intervalle $[a;+\infty[$ et $\ell \in \mathbb{R}$.
$\displaystyle \lim_{x \rightarrow +\infty}f(x)=\ell$ si pour tout intervalle ouvert I contenant $\ell$, il existe $x_0$ tel que pour tout $x>x_0$ on a $f(x)\in $ I
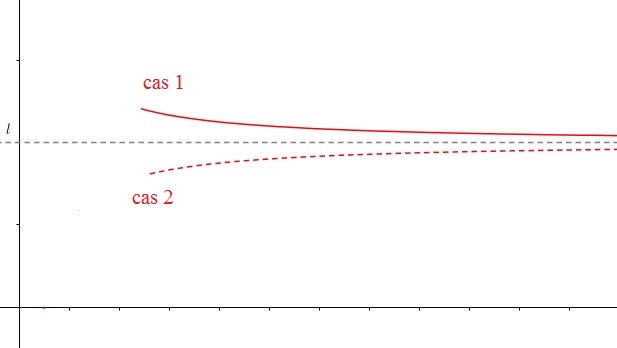
La droite d'équation $y=\ell$ est asymptote à la courbe en $+\infty$Aide
En $-\infty$ et $+\infty$, il y a un cas d'indétermination (quotient de deux limites infinies) donc il faut factoriser par le terme de plus haut degré au numérateur et au dénominateur soit $x^2$ au numérateur et $x$ au dénominateur.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements